题目内容
12.在Rt△ABC中,∠BAC=90°,AB=4,AC=3,当B、C分别在平面直角坐标系xOy的x轴、y轴上运动时,$\overrightarrow{OA}$•$\overrightarrow{OC}$的最大值是18.分析 由题意画出图形,写出$\overrightarrow{OA}$•$\overrightarrow{OC}$的数量积,由∠AOC为定值可得当$|\overrightarrow{OA}|=|\overrightarrow{OC}|$时,$\overrightarrow{OA}$•$\overrightarrow{OC}$有最大值,由此求得答案.
解答  解:由题意可知,BC=5,cos∠ABC=$\frac{4}{5}$,
解:由题意可知,BC=5,cos∠ABC=$\frac{4}{5}$,
则cos$∠AOC=\frac{4}{5}$,
$\overrightarrow{OA}$•$\overrightarrow{OC}$=$|\overrightarrow{OA}||\overrightarrow{OC}|•cos∠AOC$=$\frac{4}{5}|\overrightarrow{OA}||\overrightarrow{OC}|$.
取AC的中点D,连接OD,则当OD⊥AC时$\overrightarrow{OA}$•$\overrightarrow{OC}$有最大值.
sin∠AOD=$\sqrt{\frac{1-cos∠AOC}{2}}=\sqrt{\frac{1-\frac{4}{5}}{2}}=\frac{\sqrt{10}}{10}$.
∴$|\overrightarrow{OA}|=\frac{\frac{AC}{2}}{sin∠AOD}=\frac{\frac{3}{2}}{\frac{\sqrt{10}}{10}}=\frac{3\sqrt{10}}{2}$.
∴$\overrightarrow{OA}$•$\overrightarrow{OC}$的最大值是$\frac{4}{5}×\frac{3\sqrt{10}}{2}×\frac{3\sqrt{10}}{2}=18$.
故答案为:18.
点评 本题考查平面向量的数量积运算,考查了数形结合的解题思想方法,是中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 3 | B. | 3$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | 2 |
| A. | α | B. | α-$\frac{π}{2}$ | C. | α+$\frac{π}{2}$ | D. | α+$\frac{3π}{2}$ |
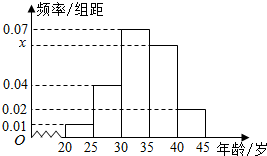 为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者,从符合条件的1000名志愿者中随机抽取100名志愿者,其中年龄频率分布直方图如图所示,其中x=3y,且年龄分组区间为:[[20,25],[25,30),[30,35),[35,40),[40,45].
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者,从符合条件的1000名志愿者中随机抽取100名志愿者,其中年龄频率分布直方图如图所示,其中x=3y,且年龄分组区间为:[[20,25],[25,30),[30,35),[35,40),[40,45].