题目内容
已知数列{an}的前n项和为Sn,且a1+2a2+3a3+…+nan=(n-1)Sn+2n(n∈N*).
(1)求数列{an}的通项公式;
(2)若p,q,r是三个互不相等的正整数,且p,q,r成等差数列,试判断ap-1,aq-1,ar-1是否成等比数列?并说明理由.
解析:(1)∵a1+2a2+3a3+…+nan=(n-1)Sn+2n,
∴当n=1时,有a1=(1-1)S1+2,解得a1=2.
由a1+2a2+3a3+…+nan=(n-1)Sn+2n,①
a1+2a2+3a3+…+nan+(n+1)an+1=nSn+1+2(n+1),②
②-①得:(n+1)an+1=nSn+ 1-(n-1)Sn+2.③
1-(n-1)Sn+2.③
由③式得:(n+1)an+1=nSn+1-(n-1)Sn+2=n(Sn+1-Sn)+Sn+2,
得an+1=Sn+2.④
当n≥2时an=Sn-1+2,⑤
⑤-④得:an+1=2an.
由a1+2a2=S2+4,得a2=4,
∴a2=2a1.
∴数列{an}是以a1=2为首项,2为公比的等比数列.
∴an=2n.
(2)∵p,q,r成等差数列,
∴p+r=2q.
假设ap-1,aq-1,ar-1成等比数列,
则(ap-1)(ar-1)=(aq-1)2,
即(2p-1)(2r-1)=(2q-1)2,
化简得:2p+2r=2×2q.(*)
∵p≠r,
∴2p+2r>2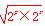 =2×2q,这与(*)式矛盾,故假设不成立.
=2×2q,这与(*)式矛盾,故假设不成立.
∴ap-1,aq-1,ar-1不是等比数列.

练习册系列答案
相关题目
 an.
an. q=________;前n项和Sn=________.
q=________;前n项和Sn=________. ,a2 015=2那么a1等于( )
,a2 015=2那么a1等于( )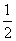 B.2 C.
B.2 C. D.-3
D.-3 过点A(2,1)和B(5,2),记an=3f(n)(n∈N*).
过点A(2,1)和B(5,2),记an=3f(n)(n∈N*). ,Tn=b1+b2+…+bn,若Tn<m(m∈Z)对n
,Tn=b1+b2+…+bn,若Tn<m(m∈Z)对n ∈N*恒成立,求m的最小值.
∈N*恒成立,求m的最小值. .
.