题目内容
函数y=
lnx的反函数为 .
| 1 |
| 2 |
考点:反函数
专题:函数的性质及应用
分析:由已知的等式变形求得x=e2y,然后把x,y互换得答案.
解答:
解:由y=
lnx,得lnx=2y,则x=e2y,
∴函数y=
lnx的反函数为f -1(x)=e2x(x∈R).
故答案为:f -1(x)=e2x(x∈R).
| 1 |
| 2 |
∴函数y=
| 1 |
| 2 |
故答案为:f -1(x)=e2x(x∈R).
点评:本题考查了函数的反函数的求法,关键是注意反函数的定义域是原函数的值域,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)是定义在R上的偶函数,且f(x+1)为奇函数.若f(2)=1,则f(1)+f(2)+f(3)+…+f(2014)=( )
| A、1 | B、2014 |
| C、0 | D、-2014 |
函数f(x)=ax+loga(x+1)在[0,1]上的最大值与最小值之和为a,则a的值为( )
A、
| ||
| B、2 | ||
| C、4 | ||
D、
|
| 3 |
| 3 |
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
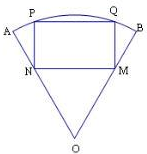 如图,在半径为1,圆心角为60°的扇形AB弧上任取一点P,作扇形的内接矩形PNMQ,使点N、M分别在半径OA、OB上,点Q在
如图,在半径为1,圆心角为60°的扇形AB弧上任取一点P,作扇形的内接矩形PNMQ,使点N、M分别在半径OA、OB上,点Q在