题目内容
19.某几何体的三视图如图所示(单位:cm),则该几何体的体积是$\frac{2\sqrt{3}}{3}$cm2.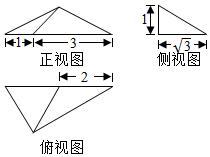
分析 根据几何体的三视图,得出该几何体是侧面垂直于底面的三棱锥,画出图形,结合图中数据即可求出它的体积.
解答 解:根据几何体的三视图得:该几何体是如图所示的三棱锥,且三棱锥的侧面PAC⊥底面ABC;
所以,该三棱锥的体积为V=$\frac{1}{3}$S△ABCh=$\frac{1}{3}$×$\frac{1}{2}$×4×$\sqrt{3}$×1=$\frac{2\sqrt{3}}{3}$.
故答案为:$\frac{2\sqrt{3}}{3}$.
点评 本题考查了空间几何体三视图的应用问题,解题的关键是根据三视图得出原几何体的结构特征,是基础题目.

练习册系列答案
相关题目
9.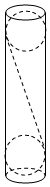 如图所示,一个圆乒乓球筒,高为20厘米,底面半径为2厘米,球桶的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度均忽略不计),一个平面与两个乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为( )
如图所示,一个圆乒乓球筒,高为20厘米,底面半径为2厘米,球桶的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度均忽略不计),一个平面与两个乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为( )
 如图所示,一个圆乒乓球筒,高为20厘米,底面半径为2厘米,球桶的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度均忽略不计),一个平面与两个乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为( )
如图所示,一个圆乒乓球筒,高为20厘米,底面半径为2厘米,球桶的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度均忽略不计),一个平面与两个乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为( )| A. | $\frac{1}{5}$ | B. | $\frac{\sqrt{15}}{4}$ | C. | $\frac{2\sqrt{6}}{5}$ | D. | $\frac{1}{4}$ |
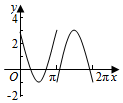
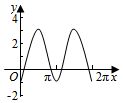
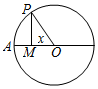 如图,圆O的半径为2,圆上一点P从A出发,绕着点O顺时针方向旋转一周,在旋转的过程中,记∠AOP为x(x∈[0,2π]),P在OA上的射影为M,记f(x)=$\overrightarrow{OP}$•$\overrightarrow{OM}$-1,那么函数f(x)的图象大致为( )
如图,圆O的半径为2,圆上一点P从A出发,绕着点O顺时针方向旋转一周,在旋转的过程中,记∠AOP为x(x∈[0,2π]),P在OA上的射影为M,记f(x)=$\overrightarrow{OP}$•$\overrightarrow{OM}$-1,那么函数f(x)的图象大致为( )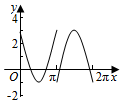

 已知椭圆x2+$\frac{{y}^{2}}{2}$=1半长轴上有一点G(0,a)(a为(0,$\sqrt{2}$)内一个常数),过G作斜率为k的直线,交椭圆于P(x1,y1),Q(x2,y2)两点.
已知椭圆x2+$\frac{{y}^{2}}{2}$=1半长轴上有一点G(0,a)(a为(0,$\sqrt{2}$)内一个常数),过G作斜率为k的直线,交椭圆于P(x1,y1),Q(x2,y2)两点. 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为4,10,则输出的a为( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为4,10,则输出的a为( )