题目内容
9.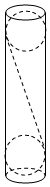 如图所示,一个圆乒乓球筒,高为20厘米,底面半径为2厘米,球桶的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度均忽略不计),一个平面与两个乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为( )
如图所示,一个圆乒乓球筒,高为20厘米,底面半径为2厘米,球桶的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度均忽略不计),一个平面与两个乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为( )| A. | $\frac{1}{5}$ | B. | $\frac{\sqrt{15}}{4}$ | C. | $\frac{2\sqrt{6}}{5}$ | D. | $\frac{1}{4}$ |
分析 设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0),由题意求出a,b,c,由此能求出该椭圆的离心率.
解答 解:不妨设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0),
由题意得$\left\{\begin{array}{l}{2a=20-4}\\{b=2}\end{array}\right.$,
解得a=8,b=2,c=$\sqrt{64-4}$=2$\sqrt{15}$,
∴该椭圆的离心率为e=$\frac{c}{a}$=$\frac{2\sqrt{15}}{8}$=$\frac{\sqrt{15}}{4}$.
故选:B.
点评 本题考查椭圆的离心率的求法,是基础题,解题时要认真审题,注意椭圆性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知曲线f(x)=ke-2x在点x=0处的切线与直线x-y-1=0垂直,若x1,x2是函数g(x)=f(x)-|1nx|的两个零点,则( )
| A. | 1<x1x2<$\sqrt{e}$ | B. | $\frac{1}{\sqrt{e}}$<x1x2<1 | C. | 2<x1x2<2$\sqrt{e}$ | D. | $\frac{2}{\sqrt{e}}$<x1x2<2 |
18.f(x)=$\frac{1}{2}$+$\frac{1}{{2}^{x}-1}$是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 是奇函数又是偶函数 | D. | 非奇函数非偶函数 |
14.已知实数x,y满足不等式组$\left\{\begin{array}{l}{lo{g}_{0.5}(2x-y)≥0}\\{1≤x≤2}\end{array}\right.$,z=x+2y,则( )
| A. | z的最大值为10,无最小值 | B. | z的最小值为3,无最大值 | ||
| C. | z的最大值为10,最小值为3 | D. | z的最大值为10,最小值为3 |