题目内容
10.设m,n是两条不同的直线,α,β是两个不同的平面,给出下列四个命题:①若m∥n,m⊥β,则n⊥β;
②若m∥α,m∥β,则α∥β;
③若m∥n,m∥β,则n∥β;
④若m⊥α,m⊥β,则α⊥β
其中真命题的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①根据线面垂直的性质定理进行判断.
②根据线面平行的判定定理进行判断.
③根据线面平行的判定定理进行判断.
④根据线面垂直和面面垂直的判定定理进行判断.
解答 解:①若m∥n,m⊥β,则n⊥β成立,故①正确;
②若m∥α,m∥β,则α∥β不一定成立,有可能相交,故②错误;
③若m∥n,m∥β,则n∥β或n?β;故③错误,
④若m⊥α,m⊥β,则α∥β,故④错误,
故正确的是①,
故选:A
点评 本题主要考查命题的真假判断,涉及空间直线和平面平行和垂直的判定,根据相应的判定定理是解决本题的关键.

练习册系列答案
相关题目
15.已知复数z=$\frac{2-3i}{1+i}$(i为虚数单位),则z在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
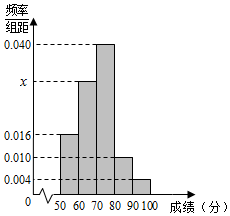 某中学举行了一次“环保知识竞赛”活动.为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出如图所示的频率分布直方图,但由于不慎丢失了部分数据.已知得分在[50,60)的有8人,在[90,100]的有2人,由此推测频率分布直方图中的x=0.03.
某中学举行了一次“环保知识竞赛”活动.为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出如图所示的频率分布直方图,但由于不慎丢失了部分数据.已知得分在[50,60)的有8人,在[90,100]的有2人,由此推测频率分布直方图中的x=0.03. 某公司从大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分).公司规定:
某公司从大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分).公司规定: