Question

2．点A、B、C、D在同一个球的球面上，${A}{B}={B}C=\sqrt{2}$，AC=2，若四面体ABCD体积的最大值为$\frac{2}{3}$，则这个球的表面积为（　　）

• A． 8π
• B． $\frac{25π}{4}$
• C． $\frac{25π}{16}$
• D． $\frac{125π}{6}$

Answer 1

分析 根据几何体的特征，判定外接球的球心，求出球的半径，即可求出球的表面积．

解答 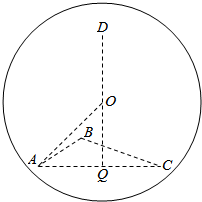解：根据题意知，△ABC是一个直角三角形，其面积为1．其所在球的小圆的圆心在斜边AC的中点上，设小圆的圆心为Q，
若四面体ABCD的体积的最大值，由于底面积S_△ABC不变，高最大时体积最大，
所以，DQ与面ABC垂直时体积最大，最大值为$\frac{1}{3}$S_△ABC×DQ=$\frac{2}{3}$，
即$\frac{1}{3}$×1×DQ=$\frac{2}{3}$，∴DQ=2，如图．
设球心为O，半径为R，则在直角△AQO中，
OA²=AQ²+OQ²，即R²=1²+（2-R）²，∴R=$\frac{5}{4}$
则这个球的表面积为：S=4π（$\frac{5}{4}$）²=$\frac{25π}{4}$
故选：B．

点评 本题考查的知识点是球内接多面体，球的表面积，其中分析出何时四面体ABCD的体积的最大值，是解答的关键．