题目内容
12.函数$f(x)=\frac{{\sqrt{2-x}}}{x-1}+{log_2}(x+1)$的定义域为( )| A. | (-1,+∞) | B. | [-1,1)∪(1,2] | C. | (-1,2] | D. | (-1,1)∪(1,2] |
分析 由$\left\{\begin{array}{l}{2-x≥0}\\{x-1≠0}\\{x+1>0}\end{array}\right.$,解得x范围即可得出.
解答 解:由$\left\{\begin{array}{l}{2-x≥0}\\{x-1≠0}\\{x+1>0}\end{array}\right.$,解得-1<x≤2,且x≠1.
∴函数f(x)的定义域为(-1,1)∪(1,2].
故选:D.
点评 本题考查了函数的定义域求法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.函数f(x)=x+$\frac{1}{x}$(x≠0)是( )
| A. | 奇函数,且在(0,1)上是增函数 | B. | 奇函数,且在(0,1)上是减函数 | ||
| C. | 偶函数,且在(0,1)上是增函数 | D. | 偶函数,且在(0,1)上是减函数 |
20.设a=20.1,b=lg$\frac{5}{2}$,c=log3$\frac{9}{10}$,则a,b,c的大小关系是( )
| A. | b>c>a | B. | a>c>b | C. | b>a>c | D. | a>b>c |
4. 如图,正方体ABCD-A1B1C1D1中,E,F分别为棱A1B1,BB1的中点,则D1E与CF的延长线交于一点,此点在直线( )
如图,正方体ABCD-A1B1C1D1中,E,F分别为棱A1B1,BB1的中点,则D1E与CF的延长线交于一点,此点在直线( )
 如图,正方体ABCD-A1B1C1D1中,E,F分别为棱A1B1,BB1的中点,则D1E与CF的延长线交于一点,此点在直线( )
如图,正方体ABCD-A1B1C1D1中,E,F分别为棱A1B1,BB1的中点,则D1E与CF的延长线交于一点,此点在直线( )| A. | AD上 | B. | B1C1上 | C. | A1D1上 | D. | BC上 |
1.函数y=1+sinx的部分图象如图所示,则该函数在[0,2π]的单调递减区间是( )


| A. | [0,π] | B. | [$\frac{π}{2}$,$\frac{3π}{2}$] | C. | [0,$\frac{3π}{2}$] | D. | [$\frac{π}{2}$,2π] |
2.点A、B、C、D在同一个球的球面上,${A}{B}={B}C=\sqrt{2}$,AC=2,若四面体ABCD体积的最大值为$\frac{2}{3}$,则这个球的表面积为( )
| A. | 8π | B. | $\frac{25π}{4}$ | C. | $\frac{25π}{16}$ | D. | $\frac{125π}{6}$ |
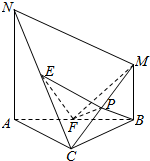 已知△ABC,$AC=BC=\sqrt{2}a$,∠ACB=90°,过点A,B作线段AN,BM分别与△ABC所在的平面垂直,且AN=AB=2BM,E,F,P分别是线段NC,AB,MC的中点.
已知△ABC,$AC=BC=\sqrt{2}a$,∠ACB=90°,过点A,B作线段AN,BM分别与△ABC所在的平面垂直,且AN=AB=2BM,E,F,P分别是线段NC,AB,MC的中点.