题目内容
已知向量
=(-1,2),
=(2,3),若
=λ
+
与
=
-
的夹角为钝角,则实数λ的取值范围是 .
| a |
| b |
| m |
| a |
| b |
| n |
| a |
| b |
考点:数量积表示两个向量的夹角
专题:平面向量及应用
分析:由夹角为钝角可得
•
<0,去除共线的情形即可.
| m |
| n |
解答:
解:∵
=(-1,2),
=(2,3),
∴
=λ
+
=(2-λ,3+2λ),
=
-
=(-3,-1),
又∵
=λ
+
与
=
-
的夹角为钝角,
∴
•
=-3(2-λ)-(3+2λ)<0,解得λ<9,
当-(2-λ)=-3(3+2λ)即λ=-1时向量共线,应去除,
∴实数λ的取值范围为:λ<9且λ≠-1
故答案为:λ<9且λ≠-1
| a |
| b |
∴
| m |
| a |
| b |
| n |
| a |
| b |
又∵
| m |
| a |
| b |
| n |
| a |
| b |
∴
| m |
| n |
当-(2-λ)=-3(3+2λ)即λ=-1时向量共线,应去除,
∴实数λ的取值范围为:λ<9且λ≠-1
故答案为:λ<9且λ≠-1
点评:本题考查平面向量的数量积和夹角,属基础题.

练习册系列答案
相关题目
设
表示复数z的共轭复数,则与“复数z为实数”不等价的说法是( )
. |
| z |
A、z=
| ||
| B、z2≥0 | ||
C、z+
| ||
| D、lmz=0(lmz表示复数z的虚部) |
将函数y=sin2x的图象向左平移
个单位,再向上平移1个单位,所得图象的函数解析式是( )
| π |
| 4 |
| A、y=cos2x | ||
B、y=1+sin(2x+
| ||
| C、y=2cos2x | ||
| D、y=2sin2x |
△ABC的内角A,B,C所对的边a,b,c满足(a+b)2-c2=4,且C=60°,则ab的值为( )
A、
| ||
B、8-4
| ||
| C、1 | ||
D、
|
在数列{an}中,若a1=2,且对任意的正整数n都有a2n=an2,则a8的值为( )
| A、256 | B、128 |
| C、64 | D、32 |
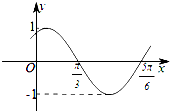 已知函数f(x)=sinωx+φ)(ω>0,0<φ≤
已知函数f(x)=sinωx+φ)(ω>0,0<φ≤