题目内容

将函数y=sin2x的图象向左平移
π
4
个单位，再向上平移1个单位，所得图象的函数解析式是（　　）
A、y=cos2x
B、y=1+sin(2x+
π
4
)
C、y=2cos2x
D、y=2sin2x
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的求值,三角函数的图像与性质
分析：首先根据函数图象的平移变换求出函数的解析式，进一步利用函数关系式的恒等变形求出结果．
解答： 解：函数y=sin2x的图象向左平移
π
4
个单位，
得到：f（x）=sin[2（x+
π
4
）]=cos2x
再把函数的图象向上平移1个单位，
得到：g（x）=cos2x+1=2cos2x
故选：C
点评：本题考查的知识要点：函数图象的平移变换，函数关系式的恒等变换，属于基础题型．
练习册系列答案
相关题目
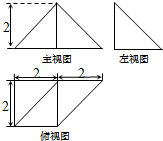
如图所示是一个四棱锥的三视图，则该几何体的体积为（　　）
 
A、4
B、
4
3
C、12
D、
2
2
3
在△ABC中，点D在BC边上，且
CD
=2
DB
，
CD
=r
AB
+s
AC
，则r+s=（　　）
A、
2
3
B、
4
3
C、1
D、0
已知函数f（x）=sin（
1
2
x+θ）-
3
cos（
1
2
x+θ）（|θ|＜
π
2
）的图象关于y中对称，则y=f（x）在下列哪个区间上是减函数（　　）
A、（0，
π
2
）
B、（
π
2
，π）
C、（-
π
2
，-
π
4
）
D、（
3π
2
，2π）
（1）若PQ是圆x2+y2=9的弦，PQ的中点是（1，2），求弦PQ的长度；
（2）已知圆心为C的圆经过点A（1，1）和B（2，-2），且圆心C在直线l：x-y+1=0上，求圆心为C的圆的标准方程．
下列哪组中的两个函数是相等函数（　　）
A、y=x，y=
5x5
B、y=
x-1
•
x+1
，y=
x2-1
C、y=1，y=
x
x
D、y=|x|，y=（
x
）2
已知向量
a
=(-1，2)，
b
=(2，3)，若
m
=λ
a
+
b
与
n
=
a
-
b
的夹角为钝角，则实数λ的取值范围是
 
．
已知函数f（x）=x3+ax2-1（a∈R是常数）．
（1）设a=-3，x=x1、x=x2是函数y=f（x）的极值点，试证明曲线y=f（x）关于点M(
x1+x2
2
，f(
x1+x2
2
))对称；
（2）是否存在常数a，使得?x∈[-1，5]，|f（x）|≤33恒成立？若存在，求常数a的值或取值范围；若不存在，请说明理由．
（注：曲线y=f（x）关于点M对称是指，对于曲线y=f（x）上任意一点P，若点P关于M的对称点为Q，则Q在曲线y=f（x）上．）
（Ⅰ）在三角形ABC中，求a=2，c=
3
，cos
B
2
=
2
5
5
角形ABC的面积S；
（Ⅱ）设函数f（x）=
3
2
cosx+
1
2
sinx+1，x∈[-
π
3
，
5π
6
]时，求f（x）的值域．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网