题目内容
 如图,在△ABC中,∠ACB=30°,D为AC上一点,∠ABD=30°,延长BD至E,连接AE、CE,若∠ECB=2∠EBC,则线段AE与CE的数量关系为
如图,在△ABC中,∠ACB=30°,D为AC上一点,∠ABD=30°,延长BD至E,连接AE、CE,若∠ECB=2∠EBC,则线段AE与CE的数量关系为考点:平面向量的基本定理及其意义
专题:平面向量及应用,立体几何
分析:如图所示,设O是△ABC的外心,连接OA,OB,OC,OD,OE.由∠ACB=30°,可得∠AOB=60°.△OAB是等边三角形.又∠ABD=30°,可得∠OBD=30°.因此BE⊥OA且平分OA.设∠OCA=α,则∠AOD=∠OAD=α.可得∠DEC=180°-∠EBC-∠ECB=3α.∠COD+∠DEC=180°.可得D、O、C、E四点共圆.因此∠DCE=∠DOE=∠DAE.于是AE=EC.
解答:
解:如图所示,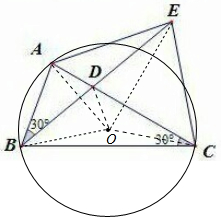 设O是△ABC的外心,连接OA,OB,OC,OD,OE.
设O是△ABC的外心,连接OA,OB,OC,OD,OE.
∵∠ACB=30°,∴∠AOB=60°.
∴△OAB是等边三角形.
又∠ABD=30°,∴∠OBD=30°.
∴BE⊥OA且平分OA.
设∠OCA=α,则∠AOD=∠OAD=α.
∴∠ODC=2α.∠COD=180°-3α.
∠OBC=∠OCB=30°-α.
∴∠EBC=30°+30°-α=60°-α.∠ECB=2∠EBC=120°-2α.∠DEC=180°-∠EBC-∠ECB=3α
∴∠COD+∠DEC=180°.
∴D、O、C、E四点共圆.
∴∠DCE=∠DOE=∠DAE.
∴AE=EC.
 设O是△ABC的外心,连接OA,OB,OC,OD,OE.
设O是△ABC的外心,连接OA,OB,OC,OD,OE.∵∠ACB=30°,∴∠AOB=60°.
∴△OAB是等边三角形.
又∠ABD=30°,∴∠OBD=30°.
∴BE⊥OA且平分OA.
设∠OCA=α,则∠AOD=∠OAD=α.
∴∠ODC=2α.∠COD=180°-3α.
∠OBC=∠OCB=30°-α.
∴∠EBC=30°+30°-α=60°-α.∠ECB=2∠EBC=120°-2α.∠DEC=180°-∠EBC-∠ECB=3α
∴∠COD+∠DEC=180°.
∴D、O、C、E四点共圆.
∴∠DCE=∠DOE=∠DAE.
∴AE=EC.
点评:本题考查了三角形外接圆的性质、等边三角形的性质、垂直平分线的性质、四点共圆的判定与性质、等腰三角形的判定,考查了推理能力和计算能力,属于难题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
f(x)=3x+3x-8,且f(1)<0,f(1.5)>0,f(1.25)<0,f(2)>0,则函数f(x)的零点落在区间( )
| A、(1,1.25) |
| B、(1.25,1.5) |
| C、(1.5,2) |
| D、不能确定 |
 如图,已知四棱柱ABCD-A1B1C1D1的棱长都为a,底面ABCD是菱形,且∠BAD=60°,侧棱A1A⊥平面ABCD,F为棱B1B的中点,M为线段AC1的中点.
如图,已知四棱柱ABCD-A1B1C1D1的棱长都为a,底面ABCD是菱形,且∠BAD=60°,侧棱A1A⊥平面ABCD,F为棱B1B的中点,M为线段AC1的中点.