题目内容
1.设关于x的方程2x2-ax-2=0的两根为α、β(α<β),函数f(x)=$\frac{4x-a}{{x}^{2}+1}$(1)求f(α)•f(β)的值;
(2)讨论函数f(x)在区间[α,β]上的单调性.
分析 (1)根据条件,由韦达定理可以求出$α+β=\frac{a}{2},αβ=-1$,而可以得到$f(α)•f(β)=\frac{16αβ-4a(α+β)+{a}^{2}}{(αβ)^{2}+(α+β)^{2}-2αβ+1}$,这样带入α+β和αβ便可得出f(α)f(β)的值;
(2)求导数得到$f′(x)=\frac{-2(2{x}^{2}-ax-2)}{({x}^{2}+1)^{2}}$,这样便可得到方程-2(2x2-ax-2)=0的两根为α,β,且α<β,这样即可判断f′(x)在区间[α,β]上的符号,从而得出f(x)在区间[α,β]上的单调性.
解答 解:(1)根据韦达定理,$α+β=\frac{a}{2},αβ=-1$;
∴$f(α)f(β)=\frac{4α-a}{{α}^{2}+1}•\frac{4β-a}{{β}^{2}+1}$
=$\frac{16αβ-4a(α+β)+{a}^{2}}{(αβ)^{2}+(α+β)^{2}-2αβ+1}$
=$\frac{-16-2{a}^{2}+{a}^{2}}{1+\frac{{a}^{2}}{4}+2+1}$
=-4;
(2)$f′(x)=\frac{4({x}^{2}+1)-2x(4x-a)}{({x}^{2}+1)^{2}}=\frac{-2(2{x}^{2}-ax-2)}{({x}^{2}+1)^{2}}$;
∵关于x的方程2x2-ax-2=0的两根为α,β;
∴方程-2(2x2-ax-2)=0的两根为α,β,且α<β;
∴α≤x≤β时,f′(x)≥0;
∴f(x)在区间[α,β]上单调递增.
点评 考查韦达定理,根据导数符号判断函数单调性的方法,商的导数的计算公式,以及二次函数的符号和对应一元二次方程实数根的关系.

 名校通行证有效作业系列答案
名校通行证有效作业系列答案| A. | $\frac{18}{19}$ | B. | $\frac{20}{19}$ | C. | $\frac{19}{20}$ | D. | $\frac{21}{20}$ |
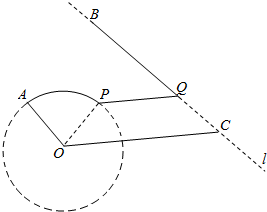 如图,B、C是海岸线l上相距50km的两个海边小城,圆O是半径为10km的某海岛小城的环岛路,A为圆O上的物资中转站,其中∠AOC=$\frac{2}{3}$π,OC=25km,且l∥OA,为使中转站A的物资运往B城,计划从A地沿环岛路至某地P,再沿水路PQ至海岸线l上Q,最后沿海岸线QB至B城修建运输线,其中PQ∥OC,Q在线段BC上.
如图,B、C是海岸线l上相距50km的两个海边小城,圆O是半径为10km的某海岛小城的环岛路,A为圆O上的物资中转站,其中∠AOC=$\frac{2}{3}$π,OC=25km,且l∥OA,为使中转站A的物资运往B城,计划从A地沿环岛路至某地P,再沿水路PQ至海岸线l上Q,最后沿海岸线QB至B城修建运输线,其中PQ∥OC,Q在线段BC上.