题目内容
16.求函数y=sin(2x-$\frac{π}{6}$)的最值,并说明取得最值时x的取值.分析 由正弦函数的最值,整体法可得.
解答 解:当2x-$\frac{π}{6}$=2kπ+$\frac{π}{2}$即x=kπ+$\frac{π}{3}$(k∈Z)时,函数取最大值1;
当2x-$\frac{π}{6}$=2kπ-$\frac{π}{2}$即x=kπ-$\frac{π}{6}$(k∈Z)时,函数取最小值-1.
点评 本题考查正弦函数的图象和最值,属基础题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
6.已知a=logπe,b=($\sqrt{6}$)-2,c=$\frac{1}{ln2}$,则a,b,c的大小关系为( )
| A. | c>b>a | B. | c>a>b | C. | a>b>c | D. | a>c>b |
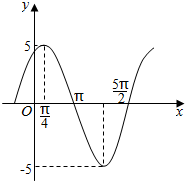 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,则函数的解析式为y=5sin($\frac{2}{3}$x+$\frac{π}{3}$).
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,则函数的解析式为y=5sin($\frac{2}{3}$x+$\frac{π}{3}$).