题目内容
20.数列{an}中,${a_1}=\frac{1}{2}$,${a_{n+1}}={a_n}+\frac{1}{(n+1)(n+2)}\begin{array}{l}{\;}{(n∈N*)}\end{array}$,则通项公式为${a}_{n}=\frac{n}{n+1}$.分析 把给出的数列递推式变形裂项,然后利用累加法求得数列通项公式.
解答 解:由${a_{n+1}}={a_n}+\frac{1}{(n+1)(n+2)}\begin{array}{l}{\;}{(n∈N*)}\end{array}$,得
${a}_{n+1}-{a}_{n}=\frac{1}{(n+1)(n+2)}=\frac{1}{n+1}-\frac{1}{n+2}$,
∴${a}_{2}-{a}_{1}=\frac{1}{2}-\frac{1}{3}$,
${a}_{3}-{a}_{2}=\frac{1}{3}-\frac{1}{4}$,
${a}_{4}-{a}_{3}=\frac{1}{4}-\frac{1}{5}$,
…
${a}_{n}-{a}_{n-1}=\frac{1}{n}-\frac{1}{n+1}$.
累加得:${a}_{n}-{a}_{1}=\frac{1}{2}-\frac{1}{n+1}=\frac{n-1}{2(n+1)}$.
又${a_1}=\frac{1}{2}$,
∴${a}_{n}=\frac{n-1}{2(n+1)}+\frac{1}{2}=\frac{n-1+n+1}{2(n+1)}=\frac{n}{n+1}$.
故答案为:${a}_{n}=\frac{n}{n+1}$.
点评 本题考查数列递推式,考查了累加法求数列的通项公式,属中档题.

练习册系列答案
相关题目
10.若α是第三象限的角,则$\frac{1}{2}$α是( )
| A. | 第一、三象限角 | B. | 第一、二象限角 | C. | 第二、三象限角 | D. | 第二、四象限角 |
8.$\int_1^2{(x-\frac{1}{x})}dx$的值是( )
| A. | 0 | B. | 1.5-ln2 | C. | 3-ln2 | D. | 1 |
10.若对于任意实数x∈[e,e2],不等式$\frac{{e}^{m}}{2}$>x-$\frac{{e}^{2}}{lnx}$恒成立,则实数的取值范围是 ( )
| A. | (-∞,-2) | B. | (-∞,2) | C. | ($\frac{1}{2}$,+∞) | D. | (2,+∞) |
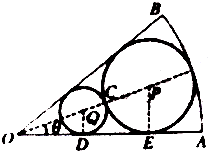 如图,在半径为1、圆心角为变量2θ(0<2θ<π)的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两半径相切并与圆P外切的小圆Q,设圆P的半径为R,圆Q的半径为r.
如图,在半径为1、圆心角为变量2θ(0<2θ<π)的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两半径相切并与圆P外切的小圆Q,设圆P的半径为R,圆Q的半径为r.