题目内容
14.已知某种物经过1000年衰减后,含量变为原来的80%,问多少年后该物质含量为原来的一半?分析 首先设出x年后该物质含量为原来的一半,则$0.{8}^{\frac{x}{1000}}=\frac{1}{2}$,两边取对数,求解x得答案.
解答 解:设x年后该物质含量为原来的一半
则$0.{8}^{\frac{x}{1000}}=\frac{1}{2}$,
即$\frac{x}{1000}•lg0.8=lg0.5$,
∴x=1000×$\frac{lg0.5}{lg0.8}$≈3000(年).
点评 本题考查对数的运算性质,关键是对题意的理解,是基础题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
4.边长为1的正方形ABCD,将△ABC沿对角线AC折起,使△ABD为正三角形,则直线BD和平面ABC所成的角的大小为( )
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
6.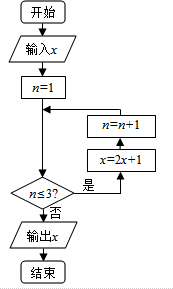 在闭区间[-4,6]上随机取出-个数x,执行如右图所示的程序框图,则输出的x不小于39的概率为( )
在闭区间[-4,6]上随机取出-个数x,执行如右图所示的程序框图,则输出的x不小于39的概率为( )
 在闭区间[-4,6]上随机取出-个数x,执行如右图所示的程序框图,则输出的x不小于39的概率为( )
在闭区间[-4,6]上随机取出-个数x,执行如右图所示的程序框图,则输出的x不小于39的概率为( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |