题目内容
4．边长为1的正方形ABCD，将△ABC沿对角线AC折起，使△ABD为正三角形，则直线BD和平面ABC所成的角的大小为（ ）| A． | 90° | B． | 60° | C． | 45° | D． | 30° |
分析 取AC的中点O，连接BO，DO，判断AC与BD的关系，即可求解直线BD和平面ABC所成的角的大小．
解答 
解：取AC的中点O，连接BO，DO，由题意，AC⊥BO，AC⊥DO，∴AC⊥平面DOB，DB
在平面ADC上的射影为：DO，BO=DO=$\frac{\sqrt{2}}{2}$，
因为△ABD为正三角形，AB=AD=DB=1，由已知可得AO=OB=OD，
∴△OBD是等腰直角三角形，
直线BD和平面ABC所成的角的大小为：45°．
故选：C．
点评 本题考查折叠问题，空间几何体的直线与平面所成角的求法，考查空间想象能力以及计算能力．
练习册系列答案
相关题目
12．等腰梯形ABCD，上底CD=1，腰AD=CB=$\sqrt{2}$，下底AB=3，以下底所在直线为x轴，则由斜二侧画法画出的直观图A′B′C′D′的面积为（ ）
| A． | $\frac{{\sqrt{2}}}{2}$ | B． | $\sqrt{2}$ | C． | $\frac{{\sqrt{2}}}{4}$ | D． | 2 |
19．不等式-x2+4x+5＜0的解集是（ ）
| A． | {x|x＞5或x＜-1} | B． | {x|x≥5或x≤-1} | C． | {x|-1＜x＜5} | D． | {x|-1≤x≤5} |
9．与-457°角的终边相同的角的集合是（ ）
| A． | {α|α=475°+k•360°，k∈Z} | B． | α|α=97°+k•360°，k∈Z} | ||
| C． | α|α=263°+k•360°，k∈Z} | D． | α|α=-263°+k•360°，k∈Z} |
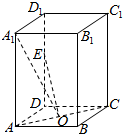如图所示，在长方体体ABCD-A1B1C1D1中，O为AC的中点．