题目内容
16．
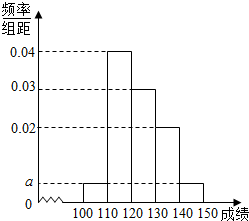贵阳市某中学高三第一次摸底考试中100名学生数学成绩的频率分布直方图如图所示，其中成绩分组区间是[100，110），[110，120），[120，130），[130，140），[140，150]．（Ⅰ）求图中a的值；
（Ⅱ）根据频率分布直方图，估计这100名学生数学成绩的平均分；
（Ⅲ）若这100名学生数学成绩某些分数段的人数（x）与语文成绩相应分数段的人数（y）之比如下表所示，求语文成绩在[100，140）之外的人数．
| 分数段 | [100，110） | [110，120） | [120，130） | [130，140） |
| x：y | 1：1 | 2：1 | 3：4 | 4：5 |
分析 （1）由频率分布直方图中频率之和为1，能求出a．
（2）平均数是频率分布直方图的重心，等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标．
（3）由已知条件分别求出数学成绩在[100，110）、[110，120）、[120，130）、[130，140）的人数，由此能求出数学成绩在[140，150）之外的人数．
解答 （本小题满分12分）
解：（1）由频率分布直方图得：
10（2a+0.02+0.03+0.04）=1，
解得a=0.005．
（2）由频率分布直方图，得，这100名学生语文成绩的平均分为：
105×0.05+115×0.4+125×0.3+135×0.2+145×0.05=123（分）．
（3）数学成绩在[100，110）的人数为：100×0.05=5
数学成绩在[110，120）的人数为：$100×0.4×\frac{1}{2}=20$，
数学成绩在[120，130）的人数为：100×$0.3×\frac{4}{3}$=40，
数学成绩在[130，140）的人数为：100×$0.2×\frac{5}{4}$=25．
所以数学成绩在[140，150）之外的人数为：100-5-20-40-25=10人．
点评 解决频率分布直方图的问题，关键在于找出图中数据之间的关系，这些数据中，比较明显的有组距、$\frac{频率}{组距}$，间接的有频率，小长方形的面积，合理使用这些数据，再结合两个等量关系：小长方形的面积等于频率，小长方形的面积之和等于1，因此频率之和为1；平均数是频率分布直方图的重心，等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标；频率分布直方图中，注意小矩形的高是$\frac{频率}{组距}$，而不是频率．
练习册系列答案
相关题目
4．设命题p：?x0∈（0，+∞），e${\;}^{{x}_{0}}$+x0=5．命题q：?x∈（0，+∞），$\frac{3}{x+1}$+x≥2$\sqrt{3}$-1．那么，下列命题为真命题的是（ ）
| A． | ￢q | B． | （￢p）∨（￢q） | C． | p∧q | D． | p∧（￢q） |
11．在空间，下列条件可以确定一个平面的是（ ）
| A． | 两条直线 | B． | 一点和一条直线 | C． | 一个三角形 | D． | 三个点 |
1．已知f（x）=$\left\{\begin{array}{l}{{x}^{2}，x＞0}\\{π，x=0}\\{0，x＜0}\end{array}\right.$，则f（-π）等于（ ）
| A． | 0 | B． | 9 | C． | π2 | D． | π |
8．将函数y=sin（2x+$\frac{π}{3}$）的图象向右平移φ（0＜φ＜$\frac{π}{2}$）个单位后的图象关于y轴对称，则φ=（ ）
| A． | $\frac{π}{12}$ | B． | $\frac{π}{6}$ | C． | $\frac{π}{3}$ | D． | $\frac{5π}{12}$ |
6．函数$f（x）={log_x}（6{x^2}-7x+2）$的定义域是（ ）
| A． | $（0{，_{\;}}\frac{1}{2}）∪（\frac{2}{3}{，_{\;}}1）∪（1{，_{\;}}+∞）$ | B． | $（-∞{，_{\;}}\frac{1}{2}）∪（\frac{2}{3}{，_{\;}}+∞）$ | ||
| C． | $（\frac{1}{2}{，_{\;}}\frac{2}{3}）$ | D． | $（0{，_{\;}}\frac{1}{2}）∪（\frac{2}{3}{，_{\;}}1）∪（1{，_{\;}}\frac{3}{2}）$ |