题目内容
15.在△ABC中,sin(C-A)=1,sinB=$\frac{1}{3}$.(I)求sinA的值;
(II)设b=$\sqrt{6}$,求△ABC的面积.
分析 (I)由已知可求C-A=$\frac{π}{2}$,结合三角形内角和定理可求A=$\frac{π}{4}$-$\frac{B}{2}$,利用两角差的正弦函数公式即可化简求值.
(Ⅱ)由正弦定理可求BC=$\frac{ACsinA}{sinB}$的值,利用两角和的正弦函数公式可求sinC的值,进而利用三角形面积公式即可计算得解.
解答 解:(I)由sin(C-A)=1,可得:C-A=$\frac{π}{2}$,且C+A=π-B,
∴A=$\frac{π}{4}$-$\frac{B}{2}$,
∴sinA=sin($\frac{π}{4}$-$\frac{B}{2}$)=$\frac{\sqrt{2}}{2}$(cos$\frac{B}{2}$-sin$\frac{B}{2}$),
∴sin2A=$\frac{1}{2}$(1-sinB)=$\frac{1}{3}$,又sinA>0,
∴sinA=$\frac{\sqrt{3}}{3}$.
(Ⅱ)由正弦定理得$\frac{AC}{sinB}=\frac{BC}{sinA}$,可得:BC=$\frac{ACsinA}{sinB}$=$\frac{\sqrt{6}×\frac{\sqrt{3}}{3}}{\frac{1}{3}}$=3$\sqrt{2}$,
又sinC=sin(A+B)=sinAcosB+cosAsinB=$\frac{\sqrt{3}}{3}×\frac{2\sqrt{2}}{3}+\frac{\sqrt{6}}{3}×\frac{1}{3}$=$\frac{\sqrt{6}}{3}$,
∴S△ABC=$\frac{1}{2}$AC•BC•sinC=$\frac{1}{2}×\sqrt{6}×3\sqrt{2}×\frac{\sqrt{6}}{3}$=3$\sqrt{2}$.
点评 本题主要考查了三角形内角和定理,两角差的正弦函数公式,正弦定理,两角和的正弦函数公式,三角形面积公式在解三角形中的应用,考查了转化思想,属于基础题.

| A. | ac>bc | B. | $\frac{b}{a}$>1 | C. | |a|>|b| | D. | ($\frac{1}{2}$)a<($\frac{1}{2}$)b |
| 环数 | 10 | 9 | 8 | 7 | 7以下 |
| 概率 | 0.25 | 0.3 | 0.2 | 0.15 | N |
(3)该射手射击一次至少射中8环的概率.
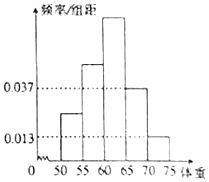 为了解今年某校高三毕业班想参军的学生体重情况,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为24.
为了解今年某校高三毕业班想参军的学生体重情况,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为24.