题目内容
15.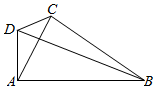 在如图所示的四边形ABCD中,∠BAD=90°,∠BCD=120°,∠BAC=60°,AC=2,记∠ABC=θ.
在如图所示的四边形ABCD中,∠BAD=90°,∠BCD=120°,∠BAC=60°,AC=2,记∠ABC=θ.(Ⅰ)求用含θ的代数式表示DC;
(Ⅱ)求△BCD面积S的最小值.
分析 (I)在△ADC中,使用正弦定理解出DC;
(II)在△ABC中,使用正弦定理解出BC,代入三角形的面积公式计算.
解答 解:(Ⅰ)在△ADC中,∠ADC=360°-90°-120°-θ=150°-θ,
由正弦定理可得$\frac{DC}{sin∠DAC}$=$\frac{AC}{sin∠ADC}$,即$\frac{DC}{sin30°}$=$\frac{2}{sin(150°-θ)}$,
于是:DC=$\frac{1}{sin(150°-θ)}$.
(Ⅱ)在△ABC中,由正弦定理得$\frac{AC}{sinθ}$=$\frac{BC}{sin60°}$,即BC=$\frac{\sqrt{3}}{sinθ}$,
由(Ⅰ)知:DC=$\frac{1}{sin(150°-θ)}$,
∴S=$\frac{1}{2}BC×CD×sin120°$=$\frac{3}{4sinθ•sin(150°-θ)}$=$\frac{3}{2sinθcosθ+2\sqrt{3}sin^2θ}$=$\frac{3}{\sqrt{3}+2sin(2θ-60°)}$.
故θ=75°时,S取得最小值6-3$\sqrt{3}$.
点评 本题考查了正弦定理在解三角形中的应用,属于中档题.

练习册系列答案
相关题目
18.已知{an}是等差数列,a1≠d,则a2+a8≠( )
| A. | a1+a9 | B. | a4+a6 | C. | 2a5 | D. | a1+a3+a6 |
3.设A,B是全集I={1,2,3,4}的子集,A={l,2},则满足A⊆B的B的个数是( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
10.已知函数f(x)=ex-2ax,函数g(x)=-x3-ax2.若不存在x1,x2∈R,使得f′(x1)=g′(x2),则实数a的取值范围为( )
| A. | (-2,3) | B. | (-6,0) | C. | [-2,3] | D. | [-6,0] |