题目内容
正方体ABCD-A1B1C1D1中,二面角C1-AB-C的平面角等于________.

试题分析:

解:如图,设正方体ABCD-A1B1C1D1的棱长为1,以DA为x轴,以DC为y轴,以DD1为z轴,建立空间直角坐标系,则A(1,0,0),B(1,1,0),C1(0,1,1),∴
 =(0,1,0),
=(0,1,0), =(-1,1,1),设面ABC1的法向量为
=(-1,1,1),设面ABC1的法向量为 =(x,y,z),∵
=(x,y,z),∵ •
• =0,
=0, •
• =0,∴y=0,-x+y+z=0,∴
=0,∴y=0,-x+y+z=0,∴ =(1,0,1),∵面ABC的法向量
=(1,0,1),∵面ABC的法向量 =(0,0,1),设二面角C1-AB-C的平面角为θ,∴cosθ=|cos<
=(0,0,1),设二面角C1-AB-C的平面角为θ,∴cosθ=|cos< ,
, >|=
>|= ,∴θ=45°,答案为45°.
,∴θ=45°,答案为45°.点评:本题考查二面角的平面角及求法,是基础题.解题时要认真审题,注意向量法的合理运用

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
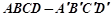 中,点
中,点 为棱
为棱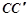 上任意一点,
上任意一点,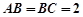 ,
,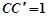 .
.

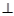 平面
平面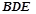 ;
;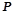 为棱
为棱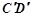 的中点,点
的中点,点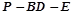 的余弦值.
的余弦值.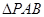 为边长为2的正三角形,底面ABCD为菱形,且平面PAB⊥平面ABCD,
为边长为2的正三角形,底面ABCD为菱形,且平面PAB⊥平面ABCD,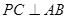 ,E为PD点上一点,满足
,E为PD点上一点,满足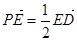
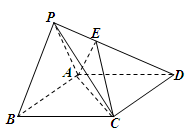
 平面ABCD;
平面ABCD;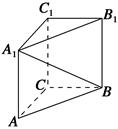
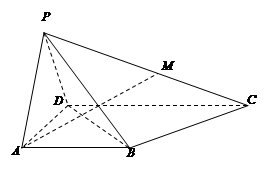
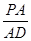 多大时,AM⊥平面PDB可能成立?
多大时,AM⊥平面PDB可能成立?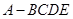 中,
中,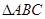 是正三角形,四边形
是正三角形,四边形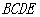 是矩形,且平面
是矩形,且平面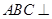 平面
平面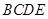 ,
,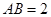 ,
,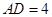 .
.
 是
是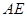 的中点,求证:
的中点,求证: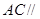 平面
平面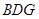 ;
;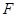 为线段
为线段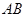 的中点,求二面角
的中点,求二面角 的正切值.
的正切值.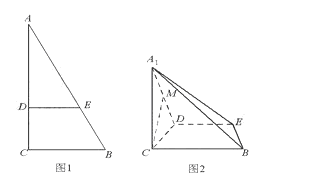
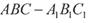 的侧棱与底面垂直,
的侧棱与底面垂直,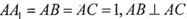 ,MN分别是
,MN分别是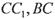 的中点,P点在
的中点,P点在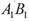 上,且满足
上,且满足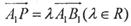
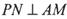
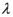 取何值时,直线PN与平面ABC所成的角
取何值时,直线PN与平面ABC所成的角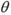 最大?并求出该最大角的正切值;
最大?并求出该最大角的正切值;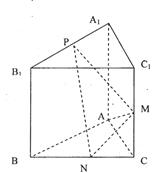
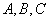 三点不共线,
三点不共线,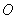 为平面
为平面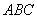 外任一点,若由
外任一点,若由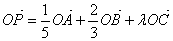 确定的一点
确定的一点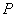 与三点
与三点 .
.