题目内容
如图所示，己知三棱柱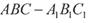
的侧棱与底面垂直，
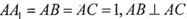，MN分别是
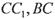的中点，P点在
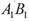上，且满足
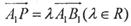
(I)证明：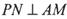
(II)当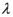
取何值时，直线PN与平面ABC所成的角
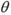最大？并求出该最大角的正切值；
(III) 在（II)条件下求P到平而AMN的距离.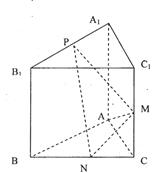
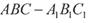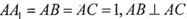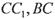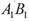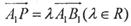
的侧棱与底面垂直，，MN分别是的中点，P点在上，且满足(I)证明：
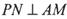
(II)当
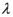取何值时，直线PN与平面ABC所成的角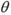最大？并求出该最大角的正切值；(III) 在（II)条件下求P到平而AMN的距离.
(Ⅰ) (12分) (Ⅰ)以
分别为
轴的正方向，建立空间直角坐标系，则
，
，
----2分
从而
，-------4分（3分）
∴
-------5分（4分）
(Ⅱ)平面ABC的一个法向量为n=（0，0，1）---------6分（5分）
则sinθ=∣cos<
>∣=
=
------8分（6分）
而
，当θ最大时，sinθ最大，tanθ最大，…理（7分）
故
时，sinθ取到最大值
时，tanθ=2 ……（8分）
(Ⅲ)设平面AMN的法向量为
="(x,y" ,z) 由 .
=0 ，.
=0
得=（1，
，2）
=(
,0,1) …（10分）
分别为轴的正方向，建立空间直角坐标系，则，， ----2分从而
，-------4分（3分）∴
-------5分（4分）(Ⅱ)平面ABC的一个法向量为n=（0，0，1）---------6分（5分）
则sinθ=∣cos<
>∣==------8分（6分）而
，当θ最大时，sinθ最大，tanθ最大，…理（7分）故
时，sinθ取到最大值时，tanθ=2 ……（8分）(Ⅲ)设平面AMN的法向量为
="(x,y" ,z) 由 .=0 ，.=0得
=（1，，2）=(,0,1) …（10分） 略
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
的底面
是正方形，
底面
是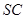
上的任意一点.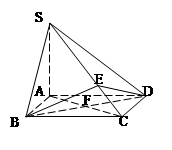
平面
；
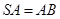时，求二面角
的大小.
，
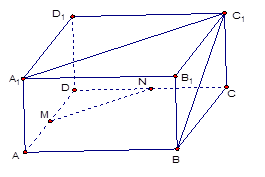
平面ACB1）作垂直于D1B的平面分别交过D1的三条棱于E、F、G．
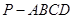中，底面ABCD是正方形，侧棱
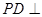底面ABCD，
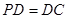，E是PC的中点，作
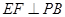交PB于点F.
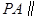平面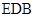
；
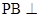平面EFD；
的大小．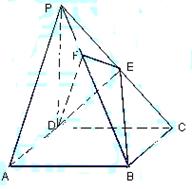
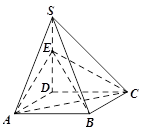
的底面是正方形,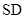
⊥平面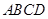
,
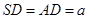,点E是SD上的点，且
.
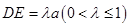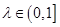，都有AC⊥BE；
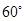，求
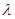的值.
