题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,且2sin2(
)+cos2C=1,a=1,b=2.
(1)求∠C和边c;
(2)若
=4
,
=
,且点P为△BMN内切圆上一点,求|
|2+|
|2+|
|2的最值.
| A+B |
| 2 |
(1)求∠C和边c;
(2)若
| BM |
| BC |
| BN |
| 3 |
| BA |
| PA |
| PB |
| PC |
考点:余弦定理,二倍角的正弦
专题:解三角形
分析:(1)已知等式利用二倍角的余弦函数公式化简,整理求出cosC的值,即可确定出C的度数;由余弦定理求出c的值即可;
(2)建立坐标系,表示出A,B,C的坐标,由
=4
,
=
,确定出M与N坐标,进而确定出△BMN的内切圆方程,设P(x,y),令
,θ∈[0,2π),利用两点间的距离公式化简原式,把表示出的x与y代入,利用正弦函数的值域确定出最大值即可.
(2)建立坐标系,表示出A,B,C的坐标,由
| BM |
| BC |
| BN |
| 3 |
| BA |
|
解答:
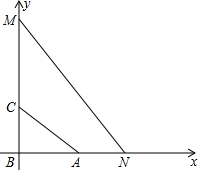 解:(1)∵2sin2
解:(1)∵2sin2
+cos2C=1,
∴cos2C=1-2sin2
=cos(A+B)=-cosC,
∴2cos2C+cosC-1=0,
∴cosC=
或cosC=-1,
∵C∈(0,π),
∴cosC=
,
∴C=
,
由余弦定理得c2=a2+b2-2abcosC=1+4-2=3,即c=
;
(2)建立坐标系,由(1)A(
,0),B(0,0),C(0,1),
由
=4
,
=
,知M(0,4),N(3,0),△BMN的内切圆方程为:(x-1)2+(y-1)2=1,
设P(x,y),则令
,θ∈[0,2π),
则|
|2+|
|2+|
|2=(x-
)2+y2+x2+y2+x2+(y-1)2
=3x2+3y2-2
x-2y+4
=11-2
+4sinθ+(6-2
)cosθ
=11-2
+
sin(θ+α)≤11-2
+
.
 解:(1)∵2sin2
解:(1)∵2sin2| A+B |
| 2 |
∴cos2C=1-2sin2
| A+B |
| 2 |
∴2cos2C+cosC-1=0,
∴cosC=
| 1 |
| 2 |
∵C∈(0,π),
∴cosC=
| 1 |
| 2 |
∴C=
| π |
| 3 |
由余弦定理得c2=a2+b2-2abcosC=1+4-2=3,即c=
| 3 |
(2)建立坐标系,由(1)A(
| 3 |
由
| BM |
| BC |
| BN |
| 3 |
| BA |
设P(x,y),则令
|
则|
| PA |
| PB |
| PC |
| 3 |
=3x2+3y2-2
| 3 |
=11-2
| 3 |
| 3 |
=11-2
| 3 |
64-24
|
| 3 |
64-24
|
点评:此题考查了余弦定理,以及正弦函数的值域,熟练掌握余弦定理是解本题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
函数f(x)=(
)x-cosx在区间[0,2π]上的零点个数是( )
| 1 |
| 2 |
| A、4 | B、3 | C、2 | D、1 |
| cos20°sin20° |
| cos225°-sin225° |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
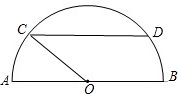 如图是一个半圆形湖面景点的示意图,已知AB为直径,且AB=2km,O为圆心,C为圆周上靠近A的一点,D为圆周上靠近B的一点,且CD∥AB,现在准备从A经过C到D建造一条观光路线,其中A到C是圆弧
如图是一个半圆形湖面景点的示意图,已知AB为直径,且AB=2km,O为圆心,C为圆周上靠近A的一点,D为圆周上靠近B的一点,且CD∥AB,现在准备从A经过C到D建造一条观光路线,其中A到C是圆弧
