题目内容
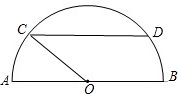 如图是一个半圆形湖面景点的示意图,已知AB为直径,且AB=2km,O为圆心,C为圆周上靠近A的一点,D为圆周上靠近B的一点,且CD∥AB,现在准备从A经过C到D建造一条观光路线,其中A到C是圆弧
如图是一个半圆形湖面景点的示意图,已知AB为直径,且AB=2km,O为圆心,C为圆周上靠近A的一点,D为圆周上靠近B的一点,且CD∥AB,现在准备从A经过C到D建造一条观光路线,其中A到C是圆弧 |
| AC |
(1)求y关于x的函数解析式,并指出该函数的定义域;
(2)求观光路线总长的最大值.
考点:根据实际问题选择函数类型
专题:应用题,导数的综合应用
分析:(1)由题意得y=1•x+1•sin(
-x)×2,化简并写出定义域(0<x<
);
(2)求导y′=1-2cos(
-x)以确定函数的单调性,从而求最大值.
| π |
| 2 |
| π |
| 2 |
(2)求导y′=1-2cos(
| π |
| 2 |
解答:
解:(1)由题意得,
y=1•x+1•sin(
-x)×2
=x+2sin(
-x),(0<x<
);
函数的定义域为{x|0<x<
};
(2)y′=1-2cos(
-x),
令y′=0解得,x=
,
故当x=
时,观光路线总长最大,
最大值为
+2×
=
+
(km).
y=1•x+1•sin(
| π |
| 2 |
=x+2sin(
| π |
| 2 |
| π |
| 2 |
函数的定义域为{x|0<x<
| π |
| 2 |
(2)y′=1-2cos(
| π |
| 2 |
令y′=0解得,x=
| π |
| 6 |
故当x=
| π |
| 6 |
最大值为
| π |
| 6 |
| ||
| 2 |
| π |
| 6 |
| 3 |
点评:本题考查了学生将实际问题转化为数学问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
三角形ABC中AB=2,AC=3,D为BC的中点,则
•
=( )
| AD |
| BC |
A、
| ||
B、-
| ||
| C、5 | ||
| D、-5 |
cosα+
sinα化简的结果可以是( )
| 3 |
| A、cos(-α) | ||||
B、2cos(
| ||||
C、
| ||||
D、2cos(
|
数列{an}的前n项和为Sn,若Sn=2an-1(n∈N*),则Tn=
+
+…+
的结果可化为( )
| 1 |
| a1a2 |
| 1 |
| a2a3 |
| 1 |
| anan+1 |
A、1-
| ||||
B、1-
| ||||
C、
| ||||
D、
|
三棱锥三条侧棱两两垂直,长度分别是1、
、2,则其外接球的表面积是( )
| 3 |
| A、8π | ||||
| B、16π | ||||
C、
| ||||
| D、32π |