题目内容
已知函数f(x)=2cos2(x-
)+2sin(x-
)sin(x+
)-1.
(1)求函数f(x)的最小正周期和单调递减区间;
(2)求函数f(x)在区间[-
,
]上的值域.
| π |
| 6 |
| π |
| 4 |
| π |
| 4 |
(1)求函数f(x)的最小正周期和单调递减区间;
(2)求函数f(x)在区间[-
| π |
| 12 |
| π |
| 2 |
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:(1)根据二倍角的正弦与余弦及辅助角公式,将解析式化为y=Asin(ωx+φ)+B的基本形式,根据正弦函数的性质,求出最小正周期和单调减区间;
(2)由x的范围求出“2x-
”的范围,根据正弦函数的单调性判断出函数的单调性,再求出端点处的函数值,进行比较后得函数的最值,即求出函数的值域.
(2)由x的范围求出“2x-
| π |
| 6 |
解答:
解:(1)∵f(x)=2cos2(x-
)+2sin(x-
)sin(x+
)-1
=cos(2x-
)+2sin(x-
)sin(x+
-
)
=cos(2x-
)+2sin(x-
)cos(x-
)
=
cos2x+
sin2x+sin(2x-
)
=
cos2x+
sin2x-cos2x
=
sin2x-
cos2x=sin(2x-
)
∴周期 T=π---------------------(6分)
由
+2kπ≤2x-
≤
+2kπ(k∈Z)得,
+kπ≤x≤
+kπ(k∈Z)
∴函数f(x)的单调递减区间为[
+kπ,
+kπ](k∈Z)-------------(8分)
(2)∵x∈[-
,
],∴2x-
∈[-
,
],-----------(9分)
∵函数f(x)=sin(2x-
)在区间[-
,
] 上单调递增,在区间[
,
]上单调递减,
∴当x=
时,f(x)取最大值f(
)=sin(
-
)=sin
=1.
又∵f(-
)=sin(-
)=-
,且f(
)=sin(π-
)=sin
=
,
∴当x=-
时,f(x)取最小值-
.
∴函数f(x)在区间[-
,
]上的值域为[-
,1]------------------------(12分)
| π |
| 6 |
| π |
| 4 |
| π |
| 4 |
=cos(2x-
| π |
| 3 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
=cos(2x-
| π |
| 3 |
| π |
| 4 |
| π |
| 4 |
=
| 1 |
| 2 |
| ||
| 2 |
| π |
| 2 |
=
| 1 |
| 2 |
| ||
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
∴周期 T=π---------------------(6分)
由
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
| π |
| 3 |
| 5π |
| 6 |
∴函数f(x)的单调递减区间为[
| π |
| 3 |
| 5π |
| 6 |
(2)∵x∈[-
| π |
| 12 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |
∵函数f(x)=sin(2x-
| π |
| 6 |
| π |
| 12 |
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
∴当x=
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 2 |
又∵f(-
| π |
| 12 |
| π |
| 3 |
| ||
| 2 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
∴当x=-
| π |
| 12 |
| ||
| 2 |
∴函数f(x)在区间[-
| π |
| 12 |
| π |
| 2 |
| ||
| 2 |
点评:本题考查了诱导公式、二倍角的正弦与余弦、辅助角公式的应用,正弦函数的周期性、利用正弦函数的单调性求给定区间上的值域问题,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
若θ为三角形一个内角,且对任意实数x,x2cosθ-4xsinθ+6>0恒成立,则θ的取值范围为( )
A、(
| ||||
B、(0,
| ||||
C、(0,
| ||||
D、(
|
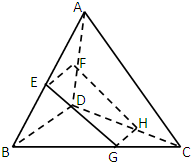 如图,已知空间四边形ABCD,E,F分别是AB,AD的中点,G,H分别是BC,CD上的点,且
如图,已知空间四边形ABCD,E,F分别是AB,AD的中点,G,H分别是BC,CD上的点,且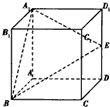 如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.
如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.