Question

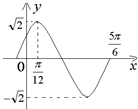函数f（x）=Asin（ωx+θ），（A＞0，ω＞0，|θ|＜

π

2

）的图象如图，求：
（1）这段曲线的函数解析式；
（2）函数g（x）=Acos（ωx+φ）（-π≤φ≤π）的图象向右平移

π

2

个单位后，与函数f（x）=Asin（ωx+θ）的图象重合，求φ；
（3）若x∈[-

2π

3

，-

π

6

]时，m+f（x+π）≥tanθ恒成立，求m的取值范围．

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式,函数y=Asin（ωx+φ）的图象变换

专题：三角函数的图像与性质

分析：（1）由图象求得A值及周期，由周期公式求得ω，再由五点作图的第二点求得φ，则函数解析式可求；
（2）把（1）中求得的A，ω值代入g（x）=Acos（ωx+φ），求出g（x）的图象向右平移

π

2

个单位所得图象的解析式，由图象与f（x）=Asin（ωx+θ）的图象重合求得φ；
（3）把（1）中求得的θ值代入m+f（x+π）≥tanθ，分离m后再由x的范围求出tanθ-f（x+π）的最大值，则m的范围可求．

解答： 解：（1）由图可知，A=

2

，

3T

4

=

5π

6

-

π

12

=

3π

4

，
∴T=π，则ω=

2π

T

=

2π

π

=2，
由五点作图第二点得：2×

π

12

+θ=

π

2

，得θ=

π

3

．
∴f（x）=

2

sin（2x+

π

3

）；
（2）g（x）=

2

cos（2x+φ）的图象向右平移

π

2

个单位得到：
y=

2

cos(2x-π+φ)=

2

sin(2x+φ-

π

2

)，
∵该函数图象与f（x）=

2

sin（2x+

π

3

）的图象重合，
∴φ-

π

2

=

π

3

+2kπ，φ=

5π

6

+2kπ，k∈Z．
∵-π≤φ≤π，
∴φ=

5π

6

；
（3）由m+f（x+π）≥tanθ恒成立，
即m≥tan

π

3

-

2

sin（2x+2π+

π

3

）=

3

-

2

sin(2x+

π

3

)恒成立．
∵x∈[-

2π

3

，-

π

6

]，
∴2x+

π

3

∈[-π，0]，
则

3

-

2

sin(2x+

π

3

)∈[

3

，

3

+

2

]，
∴m≥

3

+

2

．

点评：本题考查了由y=Asin（ωx+φ）的部分图象求函数解析式，考查了三角函数图象的平移，训练了三角恒等式的解法，由三角函数的单调性求解三角函数的值域是解答（3）的关键，是中档题．