题目内容

已知函数f（x）=ax2-x+1-a，a∈R．
（1）当a=-1时，解关于x的不等式f（x）＞0；
（2）当a≤
1
2
时，解关于x的不等式f（x）＞0．
考点：二次函数的性质
专题：函数的性质及应用
分析：（1）中把a=-1代入解不等式即可，（2）中需将a进行分区间讨论，分别解出．
解答： 解：（1）当a=-1时，f（x）=-x2-x+2，
解-x2-x+2＞0得-2＜x＜1．
（2）∵ax2-x+1-a＞0，
∴（ax+a-1）（x-1）＞0，
①0＜a≤
1
2
时，
解得：x＞1或x＜
1-a
a
，
②a=0时，
解得：x＜1，
③a＜0时，
解得：
1-a
a
＜x＜1．
点评：本题考察了二次函数的性质，不等式的解法，分类讨论思想，是一道中档题．
练习册系列答案
相关题目
下列程序框图中是执行框的图形符号的是（　　）
A、
B、
C、
D、
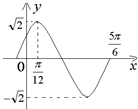函数f（x）=Asin（ωx+θ），（A＞0，ω＞0，|θ|＜
π
2
）的图象如图，求：
（1）这段曲线的函数解析式；
（2）函数g（x）=Acos（ωx+φ）（-π≤φ≤π）的图象向右平移
π
2
个单位后，与函数f（x）=Asin（ωx+θ）的图象重合，求φ；
（3）若x∈[-
2π
3
，-
π
6
]时，m+f（x+π）≥tanθ恒成立，求m的取值范围．
已知直线l经过点P（-2，1）．
（Ⅰ）若直线l的方向向量为（-2，-3），求直线l的方程；
（Ⅱ）若直线l在两坐标轴上的截距相等，求此时直线l的方程．
已知向量
a
=（3，2），
b
=（-1，2），
c
=（4，1）．
（1）求|2
b
-
a
|；
（2）若（
a
+k
c
）∥（2
b
-
a
），求实数k的值．
已知函数f（x）=ln（x+a）-x的最大值为0，其中a＞0．
（1）求a的值；
（2）若对任意x∈[0，+∞），有f（x）≥kx2成立，求实数k的最大值；
（3）证明：
n
i=1
2
2i-1
＜ln(2n+1)+2(n∈N*)．
等差数列{an}的首项为23，公差为整数，且第6项为正数，从第7项起为负数．
（1）求此数列的公差d；
（2）当前n项和Sn是正数时，求n的最大值．
已知函数f（x）=x3-3ax2+2bx在x=1处有极小值-1，试求a，b的值，
（1）并求出f（x）的单调区间
（2）在区间[-2，2]上的最大值与最小值
（3）若关于x的方程f（x）=α有3个不同实根，求实数a的取值范围．
cos420°=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网