题目内容
计算:
(1)sin2480°+cos5π+tan
+cos2(-330°)+sin(-570°)
(2)已知cos(
-α)=
,求cos(
+α)-sin2(α-
)的值.
(1)sin2480°+cos5π+tan
| 17π |
| 4 |
(2)已知cos(
| π |
| 6 |
| ||
| 3 |
| 5π |
| 6 |
| π |
| 6 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:(1)原式中的角度变形,利用诱导公式化简,再利用特殊角的三角函数值计算即可得到结果;
(2)原式中的角度变形后,利用诱导公式化简,将各自的值代入计算即可求出值.
(2)原式中的角度变形后,利用诱导公式化简,将各自的值代入计算即可求出值.
解答:
解:(1)原式=sin2(360°+120°)+cos(4π+π)+tan(4π+
)+cos2(-360°+30°)+sin(-720°+150°)
=sin2120°+cosπ+tan
+cos230°+sin150°
=
-1+1+
+
=1;
(2)∵cos(
-α)=
,
∴sin2(
-α)=
=
,
则cos(
+α)-sin2(α-
)
=cos[π-(
-α)]-sin2(
-α)
=-
-
=-
.
| π |
| 4 |
=sin2120°+cosπ+tan
| π |
| 4 |
=
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
=1;
(2)∵cos(
| π |
| 6 |
| ||
| 3 |
∴sin2(
| π |
| 6 |
1-cos2(
|
| ||
| 3 |
则cos(
| 5π |
| 6 |
| π |
| 6 |
=cos[π-(
| π |
| 6 |
| π |
| 6 |
=-
| ||
| 3 |
| ||
| 3 |
=-
| ||||
| 3 |
点评:此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
下列曲线的所有切线构成的集合中,存在无数对互相垂直的切线的曲线是( )
| A、f(x)=cosx |
| B、f(x)=ex |
| C、f(x)=x3 |
| D、f(x)=lnx |
已知函数f(x)=cos(2x+φ)(|φ|<
)的图象向左平移
个单位后的一条对称轴为x=
,则φ的取值为( )
| π |
| 2 |
| π |
| 6 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
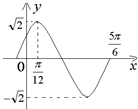 函数f(x)=Asin(ωx+θ),(A>0,ω>0,|θ|<
函数f(x)=Asin(ωx+θ),(A>0,ω>0,|θ|<