题目内容
求值：
．
| sin8°+sin7°sin75° |
| cos8°-sin7°cos75° |
考点：两角和与差的正弦函数
专题：三角函数的求值
分析：利用同角三角函数的基本关系，两角和差的正切公式把要求的式子化为 tan（45°-30°）=
，计算求得结果．
| tan45°-tan30° |
| 1+tan45°tan30° |
解答：
解：
=
=
=
=tan15°
=tan（45°-30°）=
=
=
=2-
．
| sin8°+sin7°sin75° |
| cos8°-sin7°cos75° |
| sin(15°-7°)+sin7°cos15° |
| cos(15°-7°)-sin7°sin15° |
| sin15°cos7°-cos15°sin7°+sin7°cos15° |
| cos15°cos7°+sin15°sin7°-sin7°sin15° |
| sin15°cos7° |
| cos15°cos7° |
=tan（45°-30°）=
| tan45°-tan30° |
| 1+tan45°tan30° |
1-
| ||||
1+
|
3-
| ||
3+
|
| 3 |
点评：本题主要考查同角三角函数的基本关系，两角和差的正切公式的应用，属于基础题．
练习册系列答案
相关题目
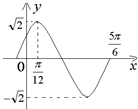函数f（x）=Asin（ωx+θ），（A＞0，ω＞0，|θ|＜