题目内容
已知直线l:mx+ny=1与曲线C:
(β为参数)无公共点,求过点(m,n)的直线与曲线ρ2=
的公共点的个数?
|
| 36 |
| 4cos2θ+9sin2θ |
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:将曲线C的参数方程化为普通方程,根据条件和点到直线的距离公式,列出m、n满足的关系式,把曲线的极坐标方程化为直角坐标系中的普通方程,判断出点(m,n)与圆、椭圆的位置关系,判断出直线与曲线的交点个数.
解答:
解:因为曲线C:
(β为参数),所以曲线C普通方程为x2+y2=
,
即C是以(0,0)为圆心、
为半径的圆,
因为直线l:mx+ny=1与曲线C无公共点,
所以
>
,化简得:m2+n2<4,
由曲线ρ2=
得:4(ρcosθ)2+9(ρsinθ)2=36,
所以直角坐标系中的方程为
+
=1,
因为点(m,n)满足m2+n2<4,
所以点(m,n)在以(0,0)为圆心、2为半径的圆内,
因为
+
=1是a=3、b=2,且焦点在x轴上的椭圆,
所以以(0,0)为圆心、2为半径的圆一定在椭圆内,
即点(m,n)在椭圆
+
=1内部,
所以过点(m,n)的直线与曲线ρ2=
的公共点的个数是2.
|
| 1 |
| 4 |
即C是以(0,0)为圆心、
| 1 |
| 2 |
因为直线l:mx+ny=1与曲线C无公共点,
所以
| 1 | ||
|
| 1 |
| 2 |
由曲线ρ2=
| 36 |
| 4cos2θ+9sin2θ |
所以直角坐标系中的方程为
| x2 |
| 9 |
| y2 |
| 4 |
因为点(m,n)满足m2+n2<4,
所以点(m,n)在以(0,0)为圆心、2为半径的圆内,
因为
| x2 |
| 9 |
| y2 |
| 4 |
所以以(0,0)为圆心、2为半径的圆一定在椭圆内,
即点(m,n)在椭圆
| x2 |
| 9 |
| y2 |
| 4 |
所以过点(m,n)的直线与曲线ρ2=
| 36 |
| 4cos2θ+9sin2θ |
点评:本题考查圆的参数方程、极坐标方程化为直角坐标系中的普通方程,以及点、直线与圆、椭圆的位置关系,属于中档题.

练习册系列答案
相关题目
已知数列{xn}满足xn+3=xn,xn+2=|xn+1-xn|(n∈N*),若x1=1,x2=a(a≤1且a≠0),则数列{xn}的前2016项的和等于( )
| A、671 | B、760 |
| C、1324 | D、1344 |
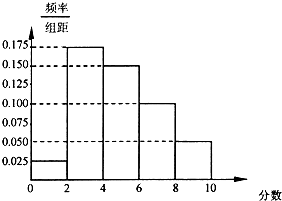 某个团购网站为了更好地满足消费者,对在其网站发布的团购产品展开了用户调查,每个用户在使用了团购产品后可以对该产品进行打分,最高分是10分.上个月该网站共卖出了100份团购产品,所有用户打分的平均分作为该产品的参考分值,将这些产品按照得分分成以下几组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10],得到的频率分布直方图如图所示.
某个团购网站为了更好地满足消费者,对在其网站发布的团购产品展开了用户调查,每个用户在使用了团购产品后可以对该产品进行打分,最高分是10分.上个月该网站共卖出了100份团购产品,所有用户打分的平均分作为该产品的参考分值,将这些产品按照得分分成以下几组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10],得到的频率分布直方图如图所示.