题目内容
数列{an}的前n项和为Sn=-2n2+n(n∈N*).
(1)求数列{an}的通项公式;
(2)求数列{an+12-an2}的前n项和Tn.
(1)求数列{an}的通项公式;
(2)求数列{an+12-an2}的前n项和Tn.
考点:数列的求和,等差数列的通项公式
专题:等差数列与等比数列
分析:(1)利用“当n=1时,a1=S1;当n≥2时,an=Sn-Sn-1”即可得出.
(2)由(Ⅰ)知,an+12-an2=(an+1-an)(an+1+an)=8(4n-1).可得数列{an+12-an2}是等差数列,利用等差数列的前n项和公式即可得出.
(2)由(Ⅰ)知,an+12-an2=(an+1-an)(an+1+an)=8(4n-1).可得数列{an+12-an2}是等差数列,利用等差数列的前n项和公式即可得出.
解答:
解:(1)当n=1时,a1=S1=-1;
当n≥2时,an=Sn-Sn-1
=(-2n2+n)-[-2(n-1)2+(n-1)]
=-4n+3.
满足a1=-1成立;
∴通项an=-4n+3(n∈N*).
(2)由(Ⅰ)知,an+12-an2=(an+1-an)(an+1+an)=8(4n-1).
∴数列{an+12-an2}是等差数列,
故Tn=8×
=16n2+8n.
当n≥2时,an=Sn-Sn-1
=(-2n2+n)-[-2(n-1)2+(n-1)]
=-4n+3.
满足a1=-1成立;
∴通项an=-4n+3(n∈N*).
(2)由(Ⅰ)知,an+12-an2=(an+1-an)(an+1+an)=8(4n-1).
∴数列{an+12-an2}是等差数列,
故Tn=8×
| n(3+4n-1) |
| 2 |
点评:本题考查了利用“当n=1时,a1=S1;当n≥2时,an=Sn-Sn-1”求数列的通项公式方法,考查了等差数列的相同公式及前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
一个圆锥的侧面展开图是中心角90°面积为S1的扇形,若圆锥的全面积是S2,则
=( )
| S1 |
| S2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=ax2+2(a-3)x+1在区间[-3,+∞)上递减,则实数a的取值范围是( )
| A、(-∞,0) | ||
B、[-
| ||
C、[-
| ||
| D、(0,+∞) |
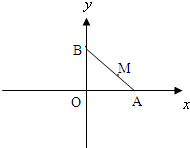 如图,线段AB的两个端点A、B分别在x轴,y轴上滑动,|AB|=3,点M是线段AB上一点,且|AM|=1点M随线段AB的滑动而运动.
如图,线段AB的两个端点A、B分别在x轴,y轴上滑动,|AB|=3,点M是线段AB上一点,且|AM|=1点M随线段AB的滑动而运动.