题目内容
5.若θ是第三象限角,且$\sqrt{1+sinθ}$=cos$\frac{θ}{2}$+sin$\frac{θ}{2}$,则$\frac{θ}{2}$是( )| A. | 第二、四象限 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
分析 由条件可得kπ+$\frac{π}{2}$<$\frac{θ}{2}$<kπ+$\frac{3π}{4}$,再根据cos$\frac{θ}{2}$+sin$\frac{θ}{2}$>0,可得$\frac{θ}{2}$是第二象限角.
解答 解:∵θ是第三象限角,∴2kπ+π<θ<2kπ+$\frac{3π}{2}$,k∈Z,即kπ+$\frac{π}{2}$<$\frac{θ}{2}$<kπ+$\frac{3π}{4}$,故$\frac{θ}{2}$是第二或第四象限角.
又∵$\sqrt{1+sinθ}$=cos$\frac{θ}{2}$+sin$\frac{θ}{2}$>0,则$\frac{θ}{2}$是第二象限角,
故选:B.
点评 本题主要考查同角三角的基本关系,象限角的表示,属于基础题.

练习册系列答案
相关题目
20.已知ω>0,函数f(x)=sin(ωx+$\frac{5π}{6}$)的一条对称轴为直线x=$\frac{π}{3}$,一个对称中心是($\frac{π}{12}$,0),则ω有( )
| A. | 最小值2 | B. | 最大值2 | C. | 最小值1 | D. | 最大值1 |
14.已知x,y满足:$\left\{\begin{array}{l}{x≤2}\\{x-2y≥0}\\{x+2y≥0}\end{array}\right.$,则$\frac{2y-x+1}{x+1}$的取值范围是( )
| A. | [-1,$\frac{1}{3}$] | B. | [-1,1] | C. | [0,$\frac{1}{3}$] | D. | [0,$\frac{4}{3}$] |
15.集合A={x∈N|-1<x<4}的真子集个数为( )
| A. | 7 | B. | 8 | C. | 15 | D. | 16 |

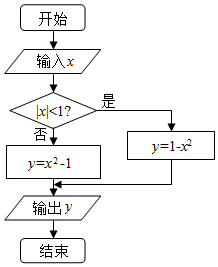 如图所示是某函数f(x)给出x的值时,求相应函数y的程序框图.
如图所示是某函数f(x)给出x的值时,求相应函数y的程序框图.