题目内容
已知函数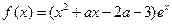 ,
,
(Ⅰ)若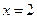 是函数
是函数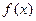 的一个极值点,求实数
的一个极值点,求实数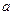 的值;
的值;
(Ⅱ)设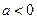 ,当
,当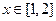 时,函数
时,函数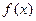 的图象恒不在直线
的图象恒不在直线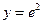 上方,求实数
上方,求实数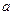 的取值范围。
的取值范围。
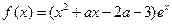 ,
,(Ⅰ)若
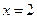 是函数
是函数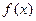 的一个极值点,求实数
的一个极值点,求实数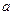 的值;
的值;(Ⅱ)设
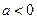 ,当
,当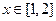 时,函数
时,函数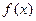 的图象恒不在直线
的图象恒不在直线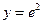 上方,求实数
上方,求实数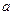 的取值范围。
的取值范围。(1)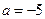 ;(2)
;(2)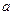 的取值范围是
的取值范围是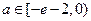
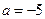 ;(2)
;(2)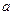 的取值范围是
的取值范围是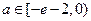
(1)由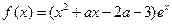 可得
可得
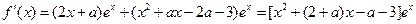
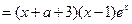
∵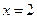 是函数
是函数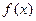 的一个极值点,∴
的一个极值点,∴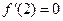
∴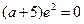 , 解得
, 解得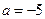
代入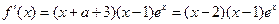 ,
,
当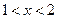 时,
时,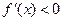 ,当
,当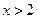 时,
时,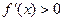
可知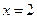 是函数
是函数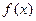 的一个极值点。 ∴
的一个极值点。 ∴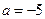
(2)要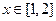 时,函数
时,函数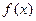 的图象恒不在直线
的图象恒不在直线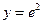 上方,
上方,
即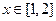 时,
时,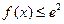 恒成立,
恒成立,
只要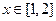 时,
时,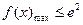 成立
成立
由(1)知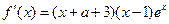 ,令
,令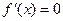 ,解得
,解得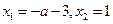
当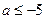 时,
时,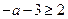 ,∴
,∴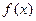 在
在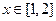 上单调递减,
上单调递减,
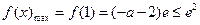 ,
,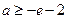 与
与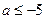 矛盾,舍去
矛盾,舍去
当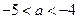 时,
时,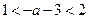 ,
,
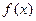 在
在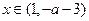 上单调递减,在
上单调递减,在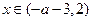 上单调递增
上单调递增
∴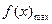 在
在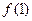 或
或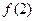 处取到
处取到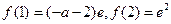
∴只要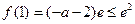 ,解得
,解得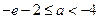
当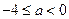 时,
时,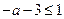 ,∴
,∴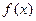 在
在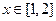 上单调递增,
上单调递增,
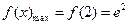 符合题意
符合题意
综上所述,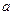 的取值范围是
的取值范围是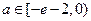
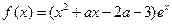 可得
可得 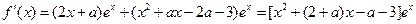
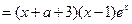
∵
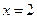 是函数
是函数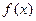 的一个极值点,∴
的一个极值点,∴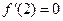
∴
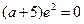 , 解得
, 解得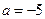
代入
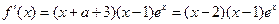 ,
,当
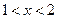 时,
时,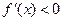 ,当
,当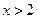 时,
时,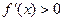
可知
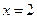 是函数
是函数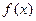 的一个极值点。 ∴
的一个极值点。 ∴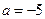
(2)要
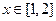 时,函数
时,函数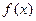 的图象恒不在直线
的图象恒不在直线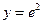 上方,
上方,即
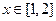 时,
时,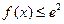 恒成立,
恒成立,只要
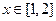 时,
时,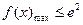 成立
成立 由(1)知
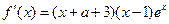 ,令
,令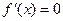 ,解得
,解得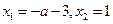
当
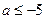 时,
时,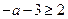 ,∴
,∴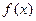 在
在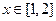 上单调递减,
上单调递减,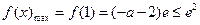 ,
,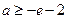 与
与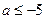 矛盾,舍去
矛盾,舍去当
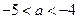 时,
时,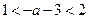 ,
,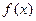 在
在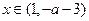 上单调递减,在
上单调递减,在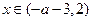 上单调递增
上单调递增∴
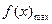 在
在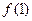 或
或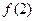 处取到
处取到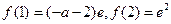
∴只要
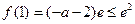 ,解得
,解得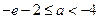
当
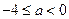 时,
时,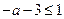 ,∴
,∴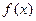 在
在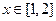 上单调递增,
上单调递增,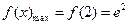 符合题意
符合题意 综上所述,
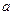 的取值范围是
的取值范围是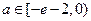

练习册系列答案
相关题目
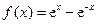 .
.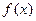 的导数
的导数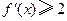 ;
;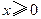 都有
都有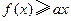 ,求
,求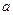 的取值范围.
的取值范围.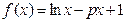
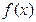 的极值点
的极值点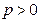 时,若对任意的
时,若对任意的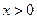 ,恒有
,恒有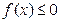 ,求
,求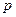 的取值范围
的取值范围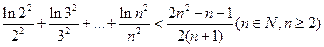
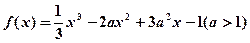 。
。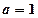 时,求函数
时,求函数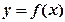 的单调增区间;
的单调增区间;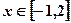 , 恒有
, 恒有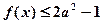 ,求
,求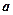 的取值范围。
的取值范围。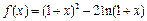 .
.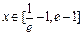 时,不等式f (x)<m恒成立,求实数m的取值范围;
时,不等式f (x)<m恒成立,求实数m的取值范围;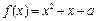 在区间[0, 2]上恰好有两个相异的实根,求实数a的取值范围.
在区间[0, 2]上恰好有两个相异的实根,求实数a的取值范围.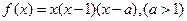
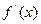 ; 并证明
; 并证明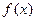 有两个不同的极值点
有两个不同的极值点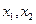 ;
; 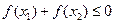 成立,求
成立,求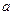 的取值范围.
的取值范围.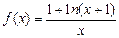
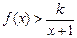 恒成立,求正整数k的最大值.
恒成立,求正整数k的最大值.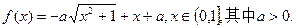
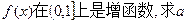 的取值范围;
的取值范围;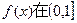 上的最大值.
上的最大值. 的图像关于原点中心对称,则
的图像关于原点中心对称,则 ( )
( ) 上为增函数
上为增函数 上为增函数,在
上为增函数,在 上为减函数
上为减函数