题目内容
18.在${(\root{3}{x}-\frac{1}{x})^n}$的展开式中,所有项的二项式系数之和为4096,则其常数项为( )| A. | -110 | B. | -220 | C. | 220 | D. | 110 |
分析 根据二项式展开式中所有项的二项式系数之和为2n求出n,再根据展开式的通项公式求出常数项的值.
解答 解:在${(\root{3}{x}-\frac{1}{x})^n}$的展开式中,所有项的二项式系数之和为
2n=4096,
则n=12;
所以${(\root{3}{x}-\frac{1}{x})}^{12}$的展开式中,
通项公式为Tr+1=${C}_{12}^{r}$•${(\root{3}{x})}^{12-r}$•${(-\frac{1}{x})}^{r}$=(-1)r•${C}_{12}^{r}$•${x}^{4-\frac{4}{3}r}$,
令4-$\frac{4}{3}$r=0,
解得r=3,
所以其常数项为(-1)3•${C}_{12}^{3}$=-220.
故选:B.
点评 本题考查了二项式展开式的所有项二项式系数和以及通项公式的应用问题,是基础题目.

练习册系列答案
相关题目
10.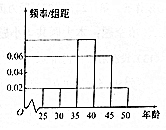 某单位N名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35).第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.
某单位N名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35).第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.
下面是年龄的分布表
(1)求正整数a、b、N的值;
(2)现要从年龄低于40岁的员工中用分层抽样的方法抽取42人,则年龄在第1、2、3组的员工人数分别是多少?
(3)为了估计该单位员工的阅读习惯,对第1、2、3组中抽出的42人是否喜欢阅读国学类书籍进行了调查,调查结果如表所示:(单位:人)
根据表中数据,能否在犯错误的概率不超过0.5%的前提下认为该单位员工“是否喜欢阅读国学类书籍和性别有关系”?
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
 某单位N名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35).第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.
某单位N名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35).第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.下面是年龄的分布表
| 区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50) |
| 人数 | 28 | a | b |
(2)现要从年龄低于40岁的员工中用分层抽样的方法抽取42人,则年龄在第1、2、3组的员工人数分别是多少?
(3)为了估计该单位员工的阅读习惯,对第1、2、3组中抽出的42人是否喜欢阅读国学类书籍进行了调查,调查结果如表所示:(单位:人)
| 喜欢阅读国学类 | 不喜欢阅读国学类 | 合计 | |
| 男 | 16 | 4 | 20 |
| 女 | 8 | 14 | 22 |
| 合计 | 24 | 18 | 42 |
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
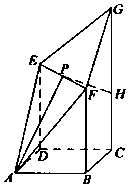 如图,四边形ABCD是边长为$\sqrt{2}$的正方形,CG⊥平面ABCD,DE∥BF∥CG,DE=BF=$\frac{3}{5}$CG.P为线段EF的中点,AP与平面ABCD所成角为60°.在线段CG上取一点H,使得GH=$\frac{3}{5}$CG.
如图,四边形ABCD是边长为$\sqrt{2}$的正方形,CG⊥平面ABCD,DE∥BF∥CG,DE=BF=$\frac{3}{5}$CG.P为线段EF的中点,AP与平面ABCD所成角为60°.在线段CG上取一点H,使得GH=$\frac{3}{5}$CG.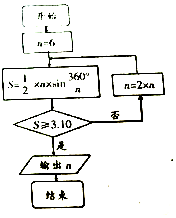 如图是利用我国古代数学家刘徽的割圆术设计的程序框图,则输出的n值为( )
如图是利用我国古代数学家刘徽的割圆术设计的程序框图,则输出的n值为( )