题目内容
求证:cos3θ+cos3(
+θ)+cos3(
-θ)=
cos3θ.
| 2π |
| 3 |
| 2π |
| 3 |
| 3 |
| 4 |
考点:两角和与差的余弦函数
专题:三角函数的求值
分析:利用两角和差的余弦公式可得:cos(
+θ)+cos(
-θ)=-cosθ.cos(
+θ)cos(
-θ)=
cos2θ-
sin2θ.左边利用立方和公式展开、同角三角函数基本关系式、3倍角公式即可得出.
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 1 |
| 4 |
| 3 |
| 4 |
解答:
证明:cos(
+θ)+cos(
-θ)=2cos
cosθ=-cosθ.
cos(
+θ)cos(
-θ)=(-
cosθ)2-(
sinθ)2=
cos2θ-
sin2θ.
∴左边=cos3θ+[cos(
+θ)+cos(
-θ)][(cos(
+θ)+cos(
-θ))2-3cos(
+θ)cos(
-θ)]
=cos3θ-cosθ[cos2θ-3(
cos2θ-
sin2θ)]
=cos3θ-cosθ(
+2sin2θ)
=cos3θ-
cosθ-2cosθ(1-cos2θ)
=3cos3θ-
cosθ
=
(4cos2θ-3cosθ)
=
cos3θ=右边.
∴左边=右边.
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
cos(
| 2π |
| 3 |
| 2π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
∴左边=cos3θ+[cos(
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
=cos3θ-cosθ[cos2θ-3(
| 1 |
| 4 |
| 3 |
| 4 |
=cos3θ-cosθ(
| 1 |
| 4 |
=cos3θ-
| 1 |
| 4 |
=3cos3θ-
| 9 |
| 4 |
=
| 3 |
| 4 |
=
| 3 |
| 4 |
∴左边=右边.
点评:本题考查了两角和差的余弦公式、立方和公式、同角三角函数基本关系式、3倍角公式,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
在下列函数中,奇函数是( )
| A、f(x)=1-x2 |
| B、f(x)=x3 |
| C、f(x)=2x |
| D、f(x)=x+1 |
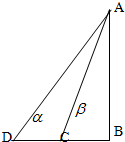 如图:D,C,B三点在地面同一直线上,DC=a,从C,D两点测得A点仰角分别是β,α(α<β),则A点离地面的高度AB等于
如图:D,C,B三点在地面同一直线上,DC=a,从C,D两点测得A点仰角分别是β,α(α<β),则A点离地面的高度AB等于