题目内容
已知A、B、C为空间三点,则经过三点( )
| A、能确定一个平面 |
| B、能确定无数个平面 |
| C、能确定一个或无数个平面 |
| D、能确定一个平面或不能确定平面 |
考点:平面的基本性质及推论
专题:空间位置关系与距离
分析:根据确定平面的公理2逐一判断即可得解.
解答:
解:当三点不共线时可唯一确定一个平面,
当三点共线时,可确定无数个平面,
故选:C.
当三点共线时,可确定无数个平面,
故选:C.
点评:本题主要考察确定平面的公理及推论.解题的关键是要对确定平面的公理及推论理解透彻.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
给定函数y=f(x)的图象如下列图中,经过原点和(1,1),且对任意an∈(0,1),由关系式an+1=f(an)得到数列{an},满足an+1>an(n∈N*),则该函数的图象为( )
A、 |
B、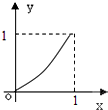 |
C、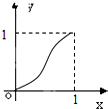 |
D、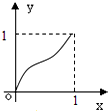 |
六个同学平均分到甲乙两个班中,分配的种数是( )
| A、20 | B、40 | C、60 | D、80 |
若方程
=x+m没有实数根,则实数m的取值范围为( )
1-
|
A、(-∞,-
| ||||
B、[-
| ||||
C、(-∞,-
| ||||
D、(
|
设直线y=x+b是曲线y=ex的一条切线,则实数b=( )
| A、-1 | B、0 | C、1 | D、2 |
已知函数f(x)在x0处可导,则
等于( )
| lim |
| △x→0 |
| f(x0-2h)-f(x0) |
| h |
| A、2f′(x0) |
| B、-f′(-x0) |
| C、-f′(x0) |
| D、-2f′(x0) |