题目内容
12.函数y=sinx-2x在R上的单调性是单调递减.分析 求函数的导数,利用函数单调性和导数之间的关系进行判断即可.
解答 解:函数的导数y′=cosx-2,
∵-1≤cosx≤1,
∴y′=cosx-2<0,
即函数y=sinx-2x在R上的单调递减,
故答案为:单调递减
点评 本题主要考查函数单调性的判断,求函数的导数,利用导数法是解决本题的关键.

练习册系列答案
相关题目
2.设a>0,b>0,则“x>a且y>b”是“x+y>a+b,且xy>ab”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
3.已知△ABC的外接圆的圆心为O,半径为1,2$\overrightarrow{OA}$+$\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{0}$,且|$\overrightarrow{OA}$|=|$\overrightarrow{AB}$|,则向量$\overrightarrow{AC}$在向量$\overrightarrow{BC}$方向上的投影为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
7.已知关于某设备的使用年限x(年)和所支出的费用y(万元),有如表所示的统计资料:
根据上表提供的数据,求出了y关于x的线性回归方程为$\stackrel{∧}{y}$=1.23x+0.08,那么统计表中t的值为( )
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | t | 6.5 | 7.0 |
| A. | 5.5 | B. | 5.0 | C. | 4.5 | D. | 4.8 |
17.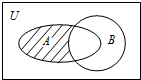 已知全集U=R,集合$A=\{\;x|\;{(\frac{1}{2})^x}≤1\;\}$,B={x|x2-6x+8≤0},则图中阴影部分所表示的集合为( )
已知全集U=R,集合$A=\{\;x|\;{(\frac{1}{2})^x}≤1\;\}$,B={x|x2-6x+8≤0},则图中阴影部分所表示的集合为( )
 已知全集U=R,集合$A=\{\;x|\;{(\frac{1}{2})^x}≤1\;\}$,B={x|x2-6x+8≤0},则图中阴影部分所表示的集合为( )
已知全集U=R,集合$A=\{\;x|\;{(\frac{1}{2})^x}≤1\;\}$,B={x|x2-6x+8≤0},则图中阴影部分所表示的集合为( )| A. | {x|x≤0} | B. | {x|2≤x≤4} | C. | {x|0<x≤2或x≥4} | D. | {x|0≤x<2或x>4} |
1.若y=f(x2),则y′等于( )
| A. | 2xf′(x2) | B. | 2xf′(x) | C. | 4x2f(x) | D. | f′(x2) |
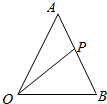 如图,在△OAB中,点P为线段AB上的一个动点(不包含端点),且满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$.
如图,在△OAB中,点P为线段AB上的一个动点(不包含端点),且满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$.