题目内容
3.已知△ABC的外接圆的圆心为O,半径为1,2$\overrightarrow{OA}$+$\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{0}$,且|$\overrightarrow{OA}$|=|$\overrightarrow{AB}$|,则向量$\overrightarrow{AC}$在向量$\overrightarrow{BC}$方向上的投影为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
分析 由题意画出图形,欲求向量$\overrightarrow{AC}$在$\overrightarrow{BC}$方向上的投影,根据投影的计算公式,只须求出这两个向量的夹角及向量$\overrightarrow{AC}$的模,借助于平面几何图形得出三角形OAB为正三角形,最后利用向量$\overrightarrow{AC}$在$\overrightarrow{BC}$方向上的投影的定义即可求解.
解答 解:∵2$\overrightarrow{OA}$+$\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{0}$,
∴$\overrightarrow{OA}$+$\overrightarrow{AB}$+$\overrightarrow{OA}$+$\overrightarrow{AC}$=$\overrightarrow{0}$,
∴$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$,
∴BC是直径,∵|$\overrightarrow{OA}$|=|$\overrightarrow{AB}$|,
∴△OAB的等边三角形,
OA=OB=AB=1,AC=$\sqrt{3}$,BC=2,
如图示: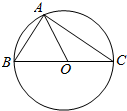 ,
,
∴向量$\overrightarrow{AC}$与向量$\overrightarrow{BC}$的夹角是30°,
∴向量$\overrightarrow{AC}$在向量$\overrightarrow{BC}$方向上的投影是|$\overrightarrow{AC}$|cos30°=$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=$\frac{3}{2}$,
故选:B.
点评 此题考查了两个向量的夹角定义,还考查向量在另外一个向量上的投影的定义及学生的分析问题的数形结合的能力.

| A. | {-1,3} | B. | {-1} | C. | {3} | D. | ∅ |
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |
| A. | 向左平移$\frac{1}{4}$个单位 | B. | 向右平移$\frac{1}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单位 | D. | 向右平移$\frac{π}{4}$个单位 |