题目内容
若tanθ=
， θ∈(0，
)，则sin(θ+
)= ．
| 1 |
| 2 |
| π |
| 2 |
| π |
| 4 |
考点：两角和与差的正弦函数,同角三角函数基本关系的运用
专题：三角函数的求值
分析：首先利用角的范围求得三角函数的值，sinθ=
cosθ=
，进一步求出sin(θ+
)=sinθcos
+
cosθsin
=
| ||
| 5 |
2
| ||
| 5 |
| π |
| 4 |
| π |
| 4 |
cosθsin
| π |
| 4 |
3
| ||
| 10 |
解答：
解：tanθ=
θ∈(0，
)
所以sinθ=
cosθ=
，
进一步求出sin(θ+
)=sinθcos
+cosθsin
=
故答案为：
| 1 |
| 2 |
| π |
| 2 |
所以sinθ=
| ||
| 5 |
2
| ||
| 5 |
进一步求出sin(θ+
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
3
| ||
| 10 |
故答案为：
3
| ||
| 10 |
点评：本题考查的知识点：三角函数的定义及应用，两角和的正弦，特殊角的三角函数值．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
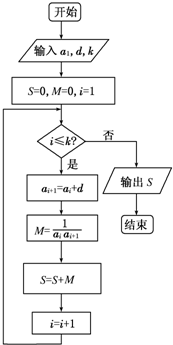已知等差数列{an}的各项均为正数，观察如图所示的程序框图，当k=5，k=10时，分别有S=| 5 |
| 11 |
| 10 |
| 21 |
| A、an=2n+1 |
| B、an=2n+3 |
| C、an=2n-1 |
| D、an=2n-3 |