题目内容
9. 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).(1)若椭圆的两个焦点与一个短轴顶点构成边长为2的正三角形,求椭圆的标准方程;
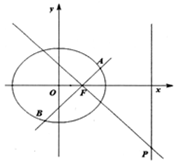
(2)过右焦点(c,0)的直线l与椭圆C交于A、B两点,过点F作l的垂线,交直线x=$\frac{{a}^{2}}{c}$于P点,若$\frac{|PF|}{|AB|}$的最小值为$\frac{b}{a}$,试求椭圆C率心率e的取值范围.
分析 (1)由已知可得:2c=2,2a=4,b2=a2-c2,解得a,b即可.
(2)设直线l的方程,A,B,P坐标,|PF|=$\frac{{b}^{2}}{c}\sqrt{1+{m}^{2}}$.联立$\left\{\begin{array}{l}{x=my+c}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,化为:(b2m2+a2)y2+2mcb2y-b4=0.|AB|=$\sqrt{(1+{m}^{2})[({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}]}$=$\frac{2a{b}^{2}(1+{m}^{2})}{{b}^{2}{m}^{2}+{a}^{2}}$.$\frac{|PF|}{|AB|}$=$\frac{{b}^{2}{m}^{2}+{a}^{2}}{2ac\sqrt{1+{m}^{2}}}$≥$\frac{b}{a}$.即可求得椭圆C率心率e的取值范围
解答 解:(1)由已知可得:2c=2,2a=4,b2=a2-c2,解得a=2,c=1,b2=3.
∴椭圆的标准方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
(2)设直线l的方程为:x=my+c,A(x1,y1),B(x2,y2).P($\frac{{a}^{2}}{c},-\frac{{b}^{2}m}{c}$)
|PF|=$\frac{{b}^{2}}{c}\sqrt{1+{m}^{2}}$.
联立$\left\{\begin{array}{l}{x=my+c}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,化为:(b2m2+a2)y2+2mcb2y-b4=0.
∴y1+y2=-$\frac{2mc{b}^{2}}{{b}^{2}{m}^{2}+{a}^{2}}$,y1•y2=$\frac{-{b}^{4}}{{b}^{2}{m}^{2}+{a}^{2}}$,
∴|AB|=$\sqrt{(1+{m}^{2})[({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}]}$=$\frac{2a{b}^{2}(1+{m}^{2})}{{b}^{2}{m}^{2}+{a}^{2}}$.
∴$\frac{|PF|}{|AB|}$=$\frac{{b}^{2}{m}^{2}+{a}^{2}}{2ac\sqrt{1+{m}^{2}}}$≥$\frac{b}{a}$.
令$\sqrt{1+{m}^{2}}=t,t≥1$,⇒b2t2-2cbt+c2≥0,
上式在t≥1时恒成立,∴椭圆C率心率e的取值范围为(0,1)
点评 本题考查椭圆的方程和性质,主要考查椭圆的离心率和方程的运用,注意联立直线方程,运用韦达定理和中点坐标公式,同时考查三点共线的方法:斜率相等,属于中档题

 应用题作业本系列答案
应用题作业本系列答案| A. | 假设当n=k(k∈N*)时,xk+yk能被x+y整除 | |
| B. | 假设当n=2k(k∈N*)时,xk+yk能被x+y整除 | |
| C. | 假设当n=2k+1(k∈N*)时,xk+yk能被x+y整除 | |
| D. | 假设当n=2k-1(k∈N*)时,x2k-1+y2k-1能被x+y整除 |
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
| 喜欢游泳 | 不喜欢游泳 | 合计 | |
| 男生 | 40 | 10 | 50 |
| 女生 | 20 | 30 | 50 |
| 合计 | 60 | 40 | 100 |
(Ⅰ)请将上述列联表补充完整,并判断是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由;
(Ⅱ)针对问卷调查的100名学生,学校决定从喜欢游泳的人中按分层抽样的方法随机抽取6人成立游泳科普知识宣传组,并在这6人中任选两人作为宣传组的组长,求这两人中至少有一名女生的概率.
参考公式:${Χ^2}=\frac{{n{{({n_{11}}{n_{22}}-{n_{12}}{n_{21}})}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}$,其中n=n11+n12+n21+n22.
参考数据:
| P(Χ2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 如图,在四棱锥P-ABCD中,PC⊥平面ABCD,底面ABCD是平行四边形,AB=BC=2a,AC=2$\sqrt{3}$a,E的PA的中点.
如图,在四棱锥P-ABCD中,PC⊥平面ABCD,底面ABCD是平行四边形,AB=BC=2a,AC=2$\sqrt{3}$a,E的PA的中点.