题目内容
14.设k∈R,函数f(x)=lnx-kx.(1)若k=2,求曲线y=f(x)在P(1,-2)处的切线方程;
(2)若f(x)无零点,求实数k的取值范围.
分析 (1)求函数f(x)的导数计算f(1),f′(1)的值,由点斜式写出切线方程即可;
(2)当k<0时,由f(1)f(ek)<0可知函数有零点,不符合题意;当k=0时,函数f(x)=lnx有唯一零点x=1有唯一零点,不符合题意;当k>0时,由单调性可知函数有最大值,由函数的最大值小于零列出不等式,解之即可.
解答 解:(1)f(x)的定义域是(0,+∞),
f′(x)=$\frac{1}{x}$-k=$\frac{1-kx}{x}$,
当k=2时,f′(1)=1-2=-1,
则切线方程为y-(-2)=-(x-1),即x+y+1=0.
(2)①若k<0时,则f′(x)>0,f(x)是区间(0,+∞)上的增函数,
∵f(1)=-k>0,f(ek)=k-kek=k(1-ek)<0,
∴f(1)•f(ek)<0,函数f(x)在区间(0,+∞)有唯一零点;
②若k=0,f(x)=lnx有唯一零点x=1;
③若k>0,令f′(x)=0,得x=$\frac{1}{k}$,
在区间(0,$\frac{1}{k}$)上,f′(x)>0,函数f(x)是增函数;
在区间($\frac{1}{k}$,+∞)上,f′(x)<0,函数f(x)是减函数;
故在区间(0,+∞)上,f(x)的极大值为f($\frac{1}{k}$)=ln$\frac{1}{k}$-1=-lnk-1,
由于f(x)无零点,须使f($\frac{1}{k}$)=-lnk-1<0,解得:k>$\frac{1}{e}$,
故所求实数k的取值范围是($\frac{1}{e}$,+∞).
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,考查函数的零点问题,是一道中档题.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
4.下列说法正确的是( )
| A. | 命题“若a≥b,则a2≥b2”的逆否命题为“若a2≤b2,则a≤b” | |
| B. | 命题“?x∈R,x2+x+1>0”的否定为“?x0∈R,x02+x0+1≤0” | |
| C. | 若p∧q为假命题,则p,q均为假命题 | |
| D. | “x=1”是“x2-3x+2=0”的必要不充分条件 |
2.已知$\overrightarrow a=({1,2}),\overrightarrow b=({m,1})$,若$\overrightarrow a⊥\overrightarrow b$,则m=( )
| A. | $-\frac{1}{2}$ | B. | -2 | C. | $\frac{1}{2}$ | D. | 2 |
19.若f(x)=sin3x+acos2x在(0,π)上存在最小值,则实数a的取值范围是( )
| A. | (0,$\frac{3}{2}$) | B. | (0,$\frac{3}{2}$] | C. | [$\frac{3}{2}$,+∞) | D. | (0,+∞) |
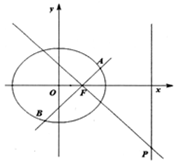 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).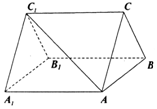 如图所示的三棱柱中,侧面ABB1A1为边长等于2的菱形,且∠AA1B1=60°,△ABC为等边三角形,面ABC⊥面ABB1A1.
如图所示的三棱柱中,侧面ABB1A1为边长等于2的菱形,且∠AA1B1=60°,△ABC为等边三角形,面ABC⊥面ABB1A1.