题目内容

已知一个正方体的所有顶点在同一个球面上，若球的表面积为9π，则正方体的棱长为
 
．
考点：球的体积和表面积
专题：综合题,空间位置关系与距离
分析：一个正方体的顶点都在同一个球面上，可得其体对角线的长度是此球体的直径，先求出直径，再求正方体的棱长．
解答： 解：∵一个正方体的顶点都在同一个球面上，若球的表面积为9π，
∴4πr2=9π，
∴球的半径为r=
3
2
，即直径为3，
令正方体的棱长为a，则根据体对角线的长度是此球体的直径有3a2=3，解得a=1．
故答案为：1．
点评：本题考查球内接多面体，求解本题关键是掌握住球内接正方体的体对角线即是球的一个直径，由此关系建立方程求出棱长，本题也考查了球的表面积公式，正方体棱长与其体对角线的关系．
练习册系列答案
相关题目
（1）用综合法证明：a2+b2+c2≥ab+bc+ca，（a，b，c∈R）；
（2）用反证法证明：若a，b，c均为实数，且a=x2-2y+
π
2
，b=y2-2z+
π
3
，c=z2-2x+
π
6
，求证a，b，c中至少有一个大于0．
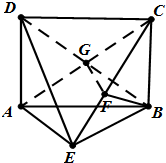如图，矩形ABCD中，AD⊥平面ABE，AE=EB=BC=2，G是AC中点，F为CE上的点，且BF⊥平面ACE．
（Ⅰ）求证：AE⊥平面BCE；
（Ⅱ）求三棱锥C-BGF的体积．
如图，在四棱锥P-ABCD中，底面ABCD是正方形，平面PAB⊥平面ABCD，
PA=PB=AB=2，M是AB的中点．
（1）证明：PM⊥平面ABCD
（2）求直线PC与平面ABCD所成的角的正切值．
求函数y=
x2+6x+14
x+1
（x＞-1）的最小值．
已知点P是椭圆
x2
6
+
y2
4
=1上任意一点，过点P作x轴的垂线，垂足为M，则线段PM的中点N（x，y）的轨迹方程为
 
．
设A={（x，y）|（x-1）2+y2≤25}，B={（x，y）|（x+1）2+y2≤25}，Ct={（x，y）||x|≤t，|y|≤t，t＞0}，则满足∁⊆（A∩B）时，t的最大值是
 
．
若函数f（x）=|x+a|-
1-x2
有两个零点，则实数a的取值范围
 
．
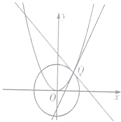如图，抛物线C：x2=2py与圆O：x2+y2=1在第一象限的交点为Q，圆O和抛物线C在点Q处的切线的斜率分别为k1，k2，若k1+k2=1，则p=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网