题目内容
已知抛物线y2=2px(p>0)的焦点为F,过点F作互相垂直的两直线AB、CD与抛物线分别相交于A、B以及C、D,若
+
=1.
(1)求此抛物线的方程.
(2)试求四边形ACBD的面积的最小值.
(3)设N(n,0)(n<0),过点N的直线与抛物线相交于P、Q两点,且
=
,试将|PQ|表示为n的表达式.
| 1 |
| |AF| |
| 1 |
| |BF| |
(1)求此抛物线的方程.
(2)试求四边形ACBD的面积的最小值.
(3)设N(n,0)(n<0),过点N的直线与抛物线相交于P、Q两点,且
| NP |
| 1 |
| 3 |
| NQ |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设直线AB的方程为y=k(x-
),联立
,得k2x2-(k2p+2p)x+k2
=0,由此得到
+
=
+
=1,从而能求出抛物线的方程.
(2)设直线AB的方程为y=k(x-1),联立
,得k2x2-(2k2+4)x+k2=0,由弦长公式得|AB|=4+
,以-
换k得|CD|=4+4k2,由此能求出四边形ACBD的面积的最小值.
(3)设P(x1,y1),Q(x2,y2)直线PQ的方程为y=t(x-n),联立
,得
y2-y-tn=0,由此能将|PQ|表示为n的表达式.
| p |
| 2 |
|
| p2 |
| 4 |
| 1 |
| |AF| |
| 1 |
| |BF| |
| 1 | ||
xA+
|
| 1 | ||
xB+
|
(2)设直线AB的方程为y=k(x-1),联立
|
| 4 |
| k2 |
| 1 |
| k |
(3)设P(x1,y1),Q(x2,y2)直线PQ的方程为y=t(x-n),联立
|
| t |
| 4 |
解答:
解:(1)设直线AB的斜率为k(k≠0),直线AB的方程为y=k(x-
),
联立
,消去y得k2x2-(k2p+2p)x+k2
=0,
从而xA+xB=p+
,xA.xB=
,
故
+
=
+
=1,
化简整理得(p2-2p)(1-
)=0,
故(p2-2p)=0,因为p>0,
所以p=2,即抛物线的方程为y2=4x.(5分)
(2)设直线AB的斜率为k(k≠0),则直线CD的斜率为-
.
直线AB的方程为y=k(x-1),
联立
,消去y得k2x2-(2k2+4)x+k2=0,
从而xA+xB=2+
,xA.xB=1,
由弦长公式得|AB|=4+
,
以-
换k得|CD|=4+4k2,
故所求面积为
|AB||CD|=(4+4k2)(4+
)×
=8(2+k2+
)≥32(当k2=1时取等号),
即面积的最小值为32.(10分)
(3)设P(x1,y1),Q(x2,y2)直线PQ的方程为y=t(x-n),
联立
,消去x得
y2-y-tn=0,
△=1-4×
(-tn)>0,即t2<-
.
又
=
,即y2=3y1,
由于y1+y2=
,y1y2=-4n,进而4y1=
,3y12=-4n,
消去y1得
=-
,
|PQ|=
=
=
(n<0).(14分)
| p |
| 2 |
联立
|
| p2 |
| 4 |
从而xA+xB=p+
| 2p |
| k2 |
| p2 |
| 4 |
故
| 1 |
| |AF| |
| 1 |
| |BF| |
| 1 | ||
xA+
|
| 1 | ||
xB+
|
化简整理得(p2-2p)(1-
| 1 |
| k2 |
故(p2-2p)=0,因为p>0,
所以p=2,即抛物线的方程为y2=4x.(5分)
(2)设直线AB的斜率为k(k≠0),则直线CD的斜率为-
| 1 |
| k |
直线AB的方程为y=k(x-1),
联立
|
从而xA+xB=2+
| 4 |
| k2 |
由弦长公式得|AB|=4+
| 4 |
| k2 |
以-
| 1 |
| k |
故所求面积为
| 1 |
| 2 |
| 4 |
| k2 |
| 1 |
| 2 |
| 1 |
| k2 |
即面积的最小值为32.(10分)
(3)设P(x1,y1),Q(x2,y2)直线PQ的方程为y=t(x-n),
联立
|
| t |
| 4 |
△=1-4×
| t |
| 4 |
| 1 |
| n |
又
| NP |
| 1 |
| 3 |
| NQ |
由于y1+y2=
| 4 |
| t |
| 4 |
| t |
消去y1得
| 1 |
| t2 |
| 4n |
| 3 |
|PQ|=
1+
|
| (y1+y2)2-4y1y2 |
1+
|
|
| 4 |
| 3 |
| 4n2-3n |
点评:本题考查抛物线方程的求法,考查四边形面积的最小值的求法,考查弦长的表达式的求法,解题时要认真审题,注意弦长公式的灵活运用.

练习册系列答案
相关题目
 如图,四棱锥P-ABCD中,底面ABCD是矩形,PA=AB=1,AD=
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA=AB=1,AD=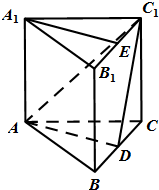 如图,正三棱柱ABC-A1B1C1的侧棱为2,底面是边长为2的等边三角形,D,E分别是线段BC,B1C1的中点.
如图,正三棱柱ABC-A1B1C1的侧棱为2,底面是边长为2的等边三角形,D,E分别是线段BC,B1C1的中点.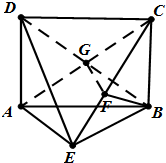 如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,G是AC中点,F为CE上的点,且BF⊥平面ACE.
如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,G是AC中点,F为CE上的点,且BF⊥平面ACE. 如图,在四棱锥P-ABCD中,底面ABCD是正方形,平面PAB⊥平面ABCD,
如图,在四棱锥P-ABCD中,底面ABCD是正方形,平面PAB⊥平面ABCD,