题目内容
7.已知a∈R,函数f(x)=lnx-ax+1.(1)讨论函数f(x)的单调性;
(2)若函数f(x)有两个不同的零点x1,x2(x1<x2),求实数a的取值范围;
(3)在(2)的条件下,求证:x1+x2>2.
分析 (1)先求导,再分类讨论,根据导数和函数单调性的关系即可求出,
(2)利用导数判断函数的单调性,以及结合零点定理即可求出a的范围;
(3)由0<x1<$\frac{1}{a}$,只要证明:f($\frac{2}{a}$-x1)>0就可以得出结论,构造函数:g(x)=f($\frac{2}{a}$-x)-f(x),利用导数即可证明.
解答 解:(1)f(x)的定义域为(0,+∞),其导数f'(x)=$\frac{1}{x}$-a.
①当a≤0时,f'(x)>0,函数在(0,+∞)上是增函数;
②当a>0时,在区间(0,$\frac{1}{a}$)上,f'(x)>0;在区间($\frac{1}{a}$,+∞)上,f'(x)<0.
∴f(x)在(0,$\frac{1}{a}$)是增函数,在($\frac{1}{a}$,+∞)是减函数.
(2)由(1)知,当a≤0时,函数f(x)在(0,+∞)上是增函数,不可能有两个零点,
当a>0时,f(x)在(0,$\frac{1}{a}$)上是增函数,在($\frac{1}{a}$,+∞)上是减函数,
此时f($\frac{1}{a}$)为函数f(x)的最大值,
当f($\frac{1}{a}$)≤0时,f(x)最多有一个零点,
∴f($\frac{1}{a}$)=ln$\frac{1}{a}$>0,解得0<a<1,
此时,$\frac{1}{e}$<$\frac{1}{a}$<$\frac{{e}^{2}}{{a}^{2}}$,且f($\frac{1}{e}$)=-1-$\frac{a}{e}$+1=-$\frac{a}{c}$<0,
f($\frac{{e}^{2}}{{a}^{2}}$)=2-2lna-$\frac{{e}^{2}}{a}$+1=3-2lna-$\frac{{e}^{2}}{a}$(0<a<1),
令F(a)=3-2lna-$\frac{{e}^{2}}{a}$,则F'(x)=-$\frac{2}{a}$+$\frac{{e}^{2}}{{a}^{2}}$=$\frac{{e}^{2}-2a}{{a}^{2}}$>0,
∴F(a)在(0,1)上单调递增,∴F(a)<F(1)=3-e2<0,即f($\frac{{e}^{2}}{{a}^{2}}$)<0,
∴a的取值范围是(0,1).
(3)由(2)可知函数f(x)在(0,$\frac{1}{a}$)是增函数,在($\frac{1}{a}$,+∞)是减函数.
分析:∵0<x1<$\frac{1}{a}$,∴$\frac{2}{a}$-x1>$\frac{1}{a}$.只要证明:f($\frac{2}{a}$-x1)>0就可以得出结论.
下面给出证明:构造函数:g(x)=f($\frac{2}{a}$-x)-f(x)=ln($\frac{2}{a}$-x)-a($\frac{2}{a}$-x)-(lnx-ax)(0<x≤$\frac{1}{a}$),
则g'(x)=$\frac{1}{x-\frac{2}{a}}$-$\frac{1}{x}$+2a=$\frac{2a(x-\frac{1}{a})^{2}}{x(x-\frac{2}{a})}$<0,
函数g(x)在区间(0,$\frac{1}{a}$]上为减函数,
∵0<x1<$\frac{1}{a}$,则g(x1)>g($\frac{1}{a}$)=0,
又f(x1)=0,
于是f($\frac{2}{a}$-x1)=ln($\frac{2}{a}$-x1)-a($\frac{2}{a}$-x1)+1-f(x1)=g(x1)>0.
又f(x2)=0,
由(1)可知x2>$\frac{2}{a}$-x1,即x1+x2>$\frac{2}{a}$>2.
点评 本题主要考查了利用导函数判断函数的单调性,以及零点定理应用与构造函数等知识点,属较难题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
| A. | a>b>c | B. | b>a>c | C. | a>c>b | D. | c>b>a |
 在长方体ABCD-A1B1C1D1中,E,F分别是AB,CD1的中点,AA1=AD=1,AB=2.
在长方体ABCD-A1B1C1D1中,E,F分别是AB,CD1的中点,AA1=AD=1,AB=2.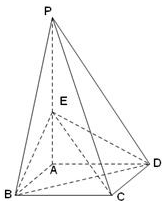 如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是侧棱PA的中点.
如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是侧棱PA的中点.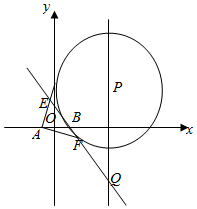 如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(-1,0)作圆Γ的两条切线分别与l交于E,F两点.
如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(-1,0)作圆Γ的两条切线分别与l交于E,F两点.