题目内容
4.设m,n是不同的直线,α、β、γ是三个不同的平面,有以下四个命题:①若m⊥α,n⊥α,则m∥n;
②若α∩γ=m,β∩γ=n,m∥n则α∥β;
③若α∥β,β∥γ,m⊥α,则m⊥γ
④若γ⊥α,γ⊥β,则α∥β.
其中正确命题的序号是( )
| A. | ①③ | B. | ②③ | C. | ③④ | D. | ①④ |
分析 根据空间线面位置关系的性质和判定定理判断或举出反例说明.
解答 解:①由于垂直于同一个平面的两条直线平行,故①正确.
②设三棱柱的三个侧面分别为α,β,γ,其中两条侧棱为m,n,显然m∥n,但α与β不平行,故②错误.
③∵α∥β∥γ,∴当m⊥α时,m⊥γ,故③正确.
④当三个平面α,β,γ两两垂直时,显然结论不成立,故④错误.
故选:A.
点评 本题考查了空间线面位置关系的判断,属于中档题.

练习册系列答案
相关题目
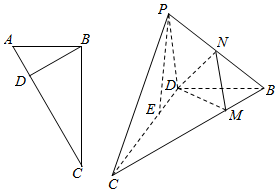 如图,直角三角形ABC中,A=60°,沿斜边AC上的高BD,将△ABD折起到△PBD的位置,点E在线段CD上.
如图,直角三角形ABC中,A=60°,沿斜边AC上的高BD,将△ABD折起到△PBD的位置,点E在线段CD上.