题目内容
9.下列函数在区间(-∞,0)上是增函数的是( )| A. | y=-$\frac{1}{x}$ | B. | y=2x2-x-1 | C. | y=|x| | D. | y=-2x-3 |
分析 利用二次函数的性质和一次函数的性质可以对B,D进行判断,利用反比例函数判断A选项,C去掉绝对值后就比较好判断了.
解答 解:A、反比例函数y=-$\frac{1}{x}$在(-∞,0)上是增函数,故A正确;
B、y=2x2-x-1,当x>$\frac{1}{4}$时,函数y单调增,x<$\frac{1}{4}$单调减,故B错误;
C、y=|x|在(-∞,0)上为减函数,在(0,+∞)上是增函数,故C错误;
D、y=-2x-3在R上是减函数,故D错误
故选A.
点评 此题主要考查函数单调性的证明,本题利用二次函数、一次函数、反比例函数的性质进行判断,会比较简单直观;

练习册系列答案
相关题目
20.数列{(-1)n(2n-1)}的前2 016项和S2016等于( )
| A. | -2 016 | B. | 2 016 | C. | -2 015 | D. | 2 015 |
17.已知等比数列{an}的首项为a1,公比为q,满足a1(q-1)<0且q>0,则( )
| A. | {an}的各项均为正数 | B. | {an}的各项均为负数 | ||
| C. | {an}为递增数列 | D. | {an}为递减数列 |
4.执行如图的程序框图,若输出的$S=\frac{31}{32}$,则输入的整数p的值为( )


| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
1.计算:log29•log38=( )
| A. | 6 | B. | 8 | C. | 10 | D. | 1 |
18.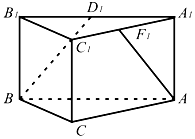 如图,直三棱柱ABC-A1B1C1中,∠BCA=90°,点D1,F1分别是A1B1,A1C1的中点,若BC=CA=2CC1,则BD1与AF1所成的角是( )
如图,直三棱柱ABC-A1B1C1中,∠BCA=90°,点D1,F1分别是A1B1,A1C1的中点,若BC=CA=2CC1,则BD1与AF1所成的角是( )
 如图,直三棱柱ABC-A1B1C1中,∠BCA=90°,点D1,F1分别是A1B1,A1C1的中点,若BC=CA=2CC1,则BD1与AF1所成的角是( )
如图,直三棱柱ABC-A1B1C1中,∠BCA=90°,点D1,F1分别是A1B1,A1C1的中点,若BC=CA=2CC1,则BD1与AF1所成的角是( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
19.下列说法中错误的是( )
| A. | 垂直于同一条直线的两条直线相互垂直 | |
| B. | 若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行 | |
| C. | 若一个平面经过另一个平面的垂线,那么这两个平面相互垂直 | |
| D. | 若一个平面内的两条相交直线与另一个平面内的相交直线分别平行,那么这两个平面相互平行 |