题目内容
19.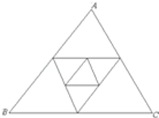 如图,已知△ABC周长为2,连接△ABC三边的中点构成第二个三角形,再连接第二个对角线三边中点构成第三个三角形,依此类推,第2003个三角形周长为( )
如图,已知△ABC周长为2,连接△ABC三边的中点构成第二个三角形,再连接第二个对角线三边中点构成第三个三角形,依此类推,第2003个三角形周长为( )| A. | $\frac{1}{2002}$ | B. | $\frac{1}{2001}$ | C. | $\frac{1}{{2}^{2002}}$ | D. | 2${\;}^{\frac{1}{2001}}$ |
分析 根据三角形的中位线定理,找规律求解,每一条中位线均为其对应的边的长度的$\frac{1}{2}$,所以新三角形周长是前一个三角形的$\frac{1}{2}$.
解答 解:△ABC周长为2,因为每条中位线均为其对应边的长度的$\frac{1}{2}$,所以:
第2个三角形对应周长为1;
第3个三角形对应的周长为$\frac{1}{2}$;
第4个三角形对应的周长为($\frac{1}{2}$)2;
…
以此类推,第n个三角形对应的周长为($\frac{1}{2}$)n-2;
所以第2003三角形对应的周长为($\frac{1}{2}$)2001.
故选:D.
点评 此题考查中位线定理,解决此题关键是找出每一个新的三角形周长是上一个三角形周长的$\frac{1}{2}$的规律,进行分析解决题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10. 如图所示是y=f(x)的导数图象,则正确的判断是( )
如图所示是y=f(x)的导数图象,则正确的判断是( )
①f(x)在(-3,1)上是增函数;
②x=-1是f(x)的极小值点;
③x=2是f(x)的极小值点;
④f(x)在(2,4)上是减函数,在(-1,2)上是增函数.
 如图所示是y=f(x)的导数图象,则正确的判断是( )
如图所示是y=f(x)的导数图象,则正确的判断是( )①f(x)在(-3,1)上是增函数;
②x=-1是f(x)的极小值点;
③x=2是f(x)的极小值点;
④f(x)在(2,4)上是减函数,在(-1,2)上是增函数.
| A. | ①②④ | B. | ②④ | C. | ③④ | D. | ①③④ |
7. 如图,在平行四边形ABCD中,点E在AB上且EB=2AE,AC与DE交于点F,则△CDF的周长与△AEF的周长之比为( )
如图,在平行四边形ABCD中,点E在AB上且EB=2AE,AC与DE交于点F,则△CDF的周长与△AEF的周长之比为( )
 如图,在平行四边形ABCD中,点E在AB上且EB=2AE,AC与DE交于点F,则△CDF的周长与△AEF的周长之比为( )
如图,在平行四边形ABCD中,点E在AB上且EB=2AE,AC与DE交于点F,则△CDF的周长与△AEF的周长之比为( )| A. | 1:3 | B. | 3:1 | C. | 1:2 | D. | 2:1 |
14.黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案,则第2016个图案中的白色地面砖有( )
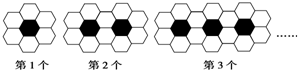

| A. | 8064块 | B. | 8066块 | C. | 8068块 | D. | 8070块 |
11.如果函数f(x)=x2-ax-3在区间(-∞,3]上单调递减,则实数a满足的条件使( )
| A. | a≤6 | B. | a≥6 | C. | a≥3 | D. | a≥-3 |
9.圆x2+y2+Dx+Ey-4=0的圆心为(-1,2),则圆的半径为( )
| A. | 6 | B. | 9 | C. | 3 | D. | 2 |