题目内容
17.设数列{an}的前n项和为Sn,已知a1=1,Sn+1=2Sn+n+1(n∈N*)(1)求数列{an}的通项公式;
(2)若bn=$\frac{{a}_{n}+1}{{a}_{n}•{a}_{n+1}}$,求数列{bn}的前n项和Tn.
分析 (1)利用递推关系可得:an+1=2an+1,变形为:an+1+1=2(an+1),利用等比数列的通项公式即可得出.
(2)利用“裂项求和”方法即可得出.
解答 解:(1)∵Sn+1=2Sn+n+1(n∈N*),
∴当n≥2时,Sn=2Sn-1+n,
∴an+1=2an+1,
变形为:an+1+1=2(an+1),
∴数列{an+1}是等比数列,公比为2,首项为2.
∴an+1=2n,
∴an=2n-1.
(2)bn=$\frac{{a}_{n}+1}{{a}_{n}•{a}_{n+1}}$=$\frac{{2}^{n}}{({2}^{n}-1)({2}^{n+1}-1)}$=$\frac{1}{{2}^{n}-1}$-$\frac{1}{{2}^{n+1}-1}$,
∴数列{bn}的前n项和Tn=$1-\frac{1}{{2}^{2}-1}$+$\frac{1}{{2}^{2}-1}-\frac{1}{{2}^{3}-1}$+…+$\frac{1}{{2}^{n}-1}$-$\frac{1}{{2}^{n+1}-1}$
=1-$\frac{1}{{2}^{n+1}-1}$.
点评 本题考查了“裂项求和”方法、数列递推关系、等比数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.已知点P为椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1上的动点,EF为圆N:x2+(y-1)2=1的任一直径,求$\overrightarrow{PE}•\overrightarrow{PF}$最大值和最小值是( )
| A. | 16,12-4$\sqrt{3}$ | B. | 17,13-4$\sqrt{3}$ | C. | 19,12-4$\sqrt{3}$ | D. | 20,13-4$\sqrt{3}$ |
5.下列命题正确的是( )
| A. | 若非零向量$\overrightarrow{a}$与$\overrightarrow{b}$的方向相同或相反,则$\overrightarrow{a}$+$\overrightarrow{b}$的方向必与$\overrightarrow{a}$,$\overrightarrow{b}$之一方向相同 | |
| B. | 在△ABC中,必有$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{CA}$=$\overrightarrow{0}$ | |
| C. | 若$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{CA}$=$\overrightarrow{0}$,则A,B,C为一个三角形的三个顶点 | |
| D. | 若$\overrightarrow{a}$与$\overrightarrow{b}$为非零向量,则|$\overrightarrow{a}$+$\overrightarrow{b}$|与|$\overrightarrow{a}$|+|$\overrightarrow{b}$|一定相等 |
12.直线$\sqrt{3}$x+3y+a=0的倾斜角为( )
| A. | 30° | B. | 60° | C. | 150° | D. | 120° |
2.函数$y={log_{\frac{1}{2}}}({{x^2}+2x-3})$的单调递增区间是( )
| A. | (-∞,-3) | B. | (-∞,-1) | C. | (-1,+∞) | D. | (1,+∞) |
9.《张丘建算经》是我国南北朝时期的一部重要数学著作,书中系统的介绍了等差数列,同类结果在三百多年后的印度才首次出现.书中有这样一个问题,大意为:某女子善于织布,后一天比前一天织的快,而且每天增加的数量相同,已知第一天织布5尺,一个月(按30天计算)总共织布390尺,问每天增加的数量为多少尺?该问题的答案为( )
| A. | $\frac{8}{29}$尺 | B. | $\frac{16}{29}$尺 | C. | $\frac{32}{29}$尺 | D. | $\frac{1}{2}$尺 |
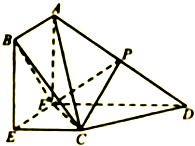 如图,四边形ABEF为矩形,四边形CEFD为直角梯形,CE∥DF,EF⊥FD,平面ABEF⊥平面CEFD,P为AD的中点,且AB=EC=$\frac{1}{2}$FD.
如图,四边形ABEF为矩形,四边形CEFD为直角梯形,CE∥DF,EF⊥FD,平面ABEF⊥平面CEFD,P为AD的中点,且AB=EC=$\frac{1}{2}$FD.