题目内容
1.某商店举行抽奖活动,袋中共有形状大小相同的三个红球三个绿球共六个球.顾客随机摸三个球,若是3个红球,则为一等奖;恰有2个红球,则为二等奖,只有1个红球,则为三等奖.则顾客中奖的概率为$\frac{19}{20}$.分析 顾客中奖的对立事件是顾客随机摸的三个球都是绿球,由此利用对立事件概率计算公式能求出顾客中奖的概率.
解答 解:由已知得:顾客中奖的对立事件是顾客随机摸的三个球都是绿球,
∴顾客中奖的概率:p=1-$\frac{{C}_{3}^{3}}{{C}_{6}^{3}}$=$\frac{19}{20}$.
故答案为:$\frac{19}{20}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意对立事件概率计算公式的合理运用.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
9.下面的命题中是真命题的是( )
| A. | 两个平面的法向量所成的角是这两个平面所成的角 | |
| B. | 设空间向量$\overrightarrow a$,$\overrightarrow b$为非零向量,若$\overrightarrow a•\overrightarrow b>0$,则$<\overrightarrow a,\overrightarrow b>$为锐角 | |
| C. | 方程mx2+ny2=1(m>0,n>0)表示的曲线是椭圆 | |
| D. | 等轴双曲线的渐近线互相垂直,离心率等于$\sqrt{2}$ |
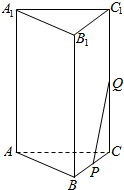 如图,在正三棱柱ABC-A1B1C1中,已知它的底面边长为10,高为20.
如图,在正三棱柱ABC-A1B1C1中,已知它的底面边长为10,高为20. 过圆外一点P作圆的切线PA(A为切点),再作割线PBC依次交圆于B,C两点.若PA=6,AC=4,BC=9,求AB的值.
过圆外一点P作圆的切线PA(A为切点),再作割线PBC依次交圆于B,C两点.若PA=6,AC=4,BC=9,求AB的值.