题目内容
已知圆O:x2+y2=2,直线l:x+2y-4=0,点P(x0,y0)在直线l上.若存在圆C上的点Q,使得∠OPQ=45°(O为坐标原点),则x0的取值范围是( )
| A、[0,1] | ||||
B、[0,
| ||||
C、[-
| ||||
D、[-
|
考点:直线与圆相交的性质
专题:直线与圆
分析:根据条件若存在圆C上的点Q,使得∠OPQ=45°(O为坐标原点),等价PO≤2即可,求出不等式的解集即可得到x0的范围
解答:
解:圆O外有一点P,圆上有一动点Q,∠OPQ在PQ与圆相切时取得最大值.
如果OP变长,那么∠OPQ可以获得的最大值将变小.可以得知,当∠OPQ=45°,且PQ与圆相切时,PO=2,
而当PO>2时,Q在圆上任意移动,∠OPQ<45°恒成立0.
因此满足PO≤2,就能保证一定存在点Q,使得∠OPQ=45°,否则,这样的点Q是不存在的;
∵点P(x0,y0)在直线x+2y-4=0上,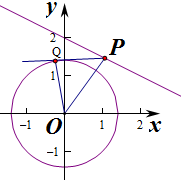 ∴x0+2y0-4=0,即y0=
∴x0+2y0-4=0,即y0=
∵|OP|2=x02+y02=x02+(
)2=
x02-2x0+4≤4,
∴
x02-2x0≤0,
解得,0≤x0≤
,
∴x0的取值范围是[0,
]
故选:B
如果OP变长,那么∠OPQ可以获得的最大值将变小.可以得知,当∠OPQ=45°,且PQ与圆相切时,PO=2,
而当PO>2时,Q在圆上任意移动,∠OPQ<45°恒成立0.
因此满足PO≤2,就能保证一定存在点Q,使得∠OPQ=45°,否则,这样的点Q是不存在的;
∵点P(x0,y0)在直线x+2y-4=0上,
 ∴x0+2y0-4=0,即y0=
∴x0+2y0-4=0,即y0=| 4-x0 |
| 2 |
∵|OP|2=x02+y02=x02+(
| 4-x0 |
| 2 |
| 5 |
| 4 |
∴
| 5 |
| 4 |
解得,0≤x0≤
| 8 |
| 5 |
∴x0的取值范围是[0,
| 8 |
| 5 |
故选:B
点评:本题考查点与圆的位置关系,利用数形结合判断出PO≤2,从而得到不等式求出参数的取值范围是解决本题的关键.综合性较强,难度较大.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
在平面直角坐标系xOy中,如果菱形OABC的边长为2,点B在y轴上,则菱形内(不含边界)的整点(横纵坐标都是整数的点)个数的取值集合是( )
| A、{1,3} |
| B、{0,1,3} |
| C、{0,1,3,4} |
| D、{0,1,2,3,4} |
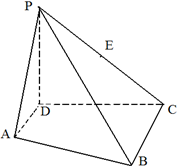 如图,已知PD⊥平面ABCD,AD⊥CD,AD∥BC,PD=DC=BC;
如图,已知PD⊥平面ABCD,AD⊥CD,AD∥BC,PD=DC=BC; 如图,某三棱柱的正视图中的实线部分是边长为4的正方形,俯视图是等边三角形,则该三棱柱的侧视图的面积为
如图,某三棱柱的正视图中的实线部分是边长为4的正方形,俯视图是等边三角形,则该三棱柱的侧视图的面积为