题目内容
19.设M是圆O:x2+y2=9上动点,直线l过M且与圆O相切,若过A(-2,0),B(2,0)两点的抛物线以直线l为准线,则抛物线焦点F的轨迹方程是( )| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{5}$=1(y≠0) | B. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{9}$=1(y≠0) | C. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1(y≠0) | D. | $\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{9}$=1(y≠0) |
分析 焦点到A和B的距离之和等于A和B分别到准线的距离和,而距离之和为A和B的中点O到准线的距离的二倍是定值,结合椭圆的定义得焦点的轨迹方程C是以A和B为焦点的椭圆.
解答 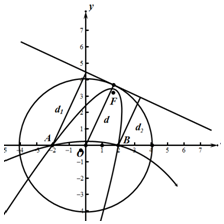 解:设A,B两点到直线l的距离分别为d1,d2,
解:设A,B两点到直线l的距离分别为d1,d2,
则d1+d2=2d=6
又因为A,B两点在抛物线上,
由定义可知|AF|+|BF|=6>|AB|,所以由椭圆定义可知,动点F的轨迹是以A,B为焦点,长轴为6的椭圆(除与x轴交点).
方程为$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1(y≠0),
故选C.
点评 本小题主要考查椭圆的定义、圆锥曲线的轨迹问题等基础知识,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.等比数列{an}前n项和为Sn,若S2=6,S4=30,则S6=( )
| A. | 62 | B. | 64 | C. | 126 | D. | 128 |
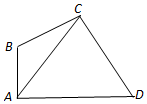 如图,在平面四边形ABCD中,AB⊥AD,AB=1,AC=$\sqrt{7}$,△ABC的面积S△ABC=$\frac{{\sqrt{3}}}{2}$,DC=$\frac{{4\sqrt{7}}}{5}$
如图,在平面四边形ABCD中,AB⊥AD,AB=1,AC=$\sqrt{7}$,△ABC的面积S△ABC=$\frac{{\sqrt{3}}}{2}$,DC=$\frac{{4\sqrt{7}}}{5}$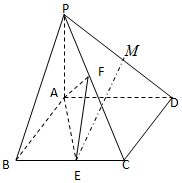 已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,E是BC中点,M是PD上的中点,F是PC上的动点.
已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,E是BC中点,M是PD上的中点,F是PC上的动点.